Почему C++ продвигает int в float, когда float не может представлять все значения int?
скажем, у меня есть следующие:
int i = 23;
float f = 3.14;
if (i == f) // do something
i будет повышен до float и два float числа будут сравниваться, но может a float представляют все int значения? Почему бы не продвигать оба int и float до double?
9 ответов
, когда int превращается в unsigned в интегральных акциях отрицательные значения также теряются (что приводит к такой забаве, как 0u < -1 быть верным).
как и большинство механизмов в C (которые наследуются в C++), обычные арифметические преобразования следует понимать с точки зрения аппаратных операций. Создатели C были хорошо знакомы с языком сборки машин, с которыми они работали, и они писали C, чтобы иметь непосредственный смысл для себя и таких людей, как сами при написании вещей, которые до этого были бы написаны в сборке (например, ядро UNIX).
теперь процессоры, как правило, не имеют инструкций смешанного типа (добавьте float в double, сравните int с float и т. д.) потому что это было бы огромной тратой недвижимости на вафлю-вам пришлось бы внедрять в столько раз больше опкодов, сколько вы хотите поддерживать разные типы. Что у вас есть только инструкции для "add int to int", "compare float to float", " multiply unsigned с неподписанным" и т. д. делает обычные арифметические преобразования необходимыми в первую очередь-они представляют собой отображение двух типов в семейство инструкций, которое имеет наибольший смысл использовать с ними.
С точки зрения того, кто привык писать машинный код низкого уровня, если у вас смешанные типы, инструкции ассемблера, которые вы, скорее всего, рассмотрите в общем случае,-это те, которые требуют наименьших преобразований. Это особенно относится к плавающим точкам, где преобразования являются дорогостоящими во время выполнения, и особенно в начале 1970-х годов, когда был разработан C, компьютеры были медленными, и когда вычисления с плавающей запятой были сделаны в программном обеспечении. Это показывает в обычных арифметических преобразованиях - только один операнд когда-либо преобразуется (за единственным исключением long/unsigned int, где long может быть преобразован в unsigned long, который не требует ничего, чтобы быть сделано на большинстве машин. Возможно, не на любом, где применяется исключение).
так, обычные арифметические преобразования написаны для того, что кодер сборки будет делать большую часть времени: у вас есть два типа, которые не подходят, преобразуйте один в другой, чтобы он это сделал. Это то, что вы сделали бы в ассемблерном коде, если бы у вас не было конкретной причины делать иначе, и людям, которые привыкли писать ассемблерный код и do есть конкретная причина, чтобы заставить другое преобразование, явно запрашивая, что преобразование является естественным. Ведь можно просто пиши
if((double) i < (double) f)
интересно отметить в этом контексте, кстати, что unsigned выше в иерархии, чем int, Так что сравнивать int С unsigned завершится сравнением без знака (отсюда 0u < -1 - чуть с самого начала). Я подозреваю, что это показатель, который люди в старые времена считали unsigned меньше как ограничение на int чем как расширение его диапазона значений: нам не нужен знак прямо сейчас, так давайте использовать дополнительные для больших диапазон значений. Вы бы использовали его, если бы у вас были основания ожидать, что int переполнение - гораздо большее беспокойство в мире 16-бит ints.
даже double может быть не в состоянии представлять все int значения, в зависимости от того, сколько бит int содержать.
почему бы не повысить как int, так и float до double?
вероятно, потому, что дороже конвертировать оба типа в double чем использовать один из операндов, который уже float, as float. Он также вводит специальные правила для операторов сравнения, несовместимые с правилами для арифметических операторов.
также нет гарантии, как будут представлены типы с плавающей запятой, поэтому было бы слепым выстрелом предположить, что преобразование int to double (или даже long double) для сравнения ничего не решают.
правила продвижения типов разработаны, чтобы быть простыми и работать предсказуемым образом. Типы В C / C++, естественно, "сортируются" по диапазон значений они могут представлять. См.этой для сведения. Хотя типы с плавающей запятой не могут представлять все целые числа, представленные целыми типами, поскольку они не могут представлять одинаковое количество значащих цифр, они могут представлять более широкий диапазон.
иметь предсказуемое поведение, при необходимости рекламных акций типов числовые типы всегда преобразуются в тип с больше диапазон, чтобы избежать переполнения в меньшей. Представьте себе:
int i = 23464364; // more digits than float can represent!
float f = 123.4212E36f; // larger range than int can represent!
if (i == f) { /* do something */ }
если преобразование было сделано в направлении интегрального типа, float f, безусловно, переполнится при преобразовании в int, что приведет к неопределенному поведению. С другой стороны, преобразование i to f только вызывает потерю точности, которая не имеет значения, так как f имеет такую же точность таким образом, все еще возможно, что сравнение будет успешным. В этот момент программист должен интерпретировать результат сравнения в соответствии с требованиями приложения.
наконец, помимо того, что числа с плавающей запятой двойной точности страдают от одной и той же проблемы, представляющей целые числа (ограниченное количество значащих цифр), использование продвижения по обоим типам приведет к более высокоточному представлению для i, а f обречен иметь оригинальная точность, поэтому сравнение не удастся, если i имеет более значительные цифры, чем f для начала. Теперь это также неопределенное поведение: сравнение может быть успешным для некоторых пар (i,f), но не для других.
can a
floatпредставляют всеintзначения?
для типичной современной системы, где обе int и float хранятся в 32 битах, нет. Что-то должно измениться. 32 бит целых чисел не сопоставляет 1-к-1 на набор одинакового размера, который включает дроби.
на
iбудет повышен доfloatи дваfloatчисла будут сравниваться...
не обязательно. Ты действительно не знаешь, что точность будет применяться. C++14 §5/12:
значения плавающих операндов и результаты плавающих выражений могут быть представлены с большей точностью и диапазоном, чем это требуется типом; типы не изменяются таким образом.
хотя i после продвижения имеет номинальный тип float значение может быть представлено с помощью double оборудование. C++ не гарантирует потерю или переполнение точности с плавающей запятой. (Это не ново в C++14; он унаследован от C с древних времен.)
почему бы не продвинуть оба
intиfloatдоdouble?
если вы хотите оптимальную точность везде, используйте double вместо этого, и вы никогда не увидите float. Или long double, но это может работать медленнее. Правила разработаны, чтобы быть относительно разумными для большинства случаев использования типов с ограниченной точностью, учитывая, что одна машина может предложить несколько альтернативных точности.
большую часть времени, быстро и свободно достаточно хорошо, поэтому машина свободна делать все, что легче всего. Это может означать округлое сравнение с одной точностью или двойную точность и отсутствие округления.
но такие правила в конечном счете являются компромиссами, и иногда они терпят неудачу. Чтобы точно указать арифметику в C++ (или C), это помогает сделать конверсии и рекламные акции явными. Многие руководства по стилю для сверхнадежного программного обеспечения запрещают использование неявных преобразований в целом, и большинство компиляторов предлагают предупреждения, которые помогут вам удалить их.
чтобы узнать о том, как эти компромиссы пришли, вы можете прочитать C обоснование документа. (Последнее издание охватывает до C99.) Это не просто бессмысленный багаж со времен PDP-11 или K&R.
интересно, что ряд ответов здесь аргументируют происхождение языка C, явно называя K&R и исторический багаж причиной того, что int преобразуется в float в сочетании с float.
это указывает вину на неправильные стороны. В K&R C не было такой вещи, как расчет поплавка. все операции с плавающей запятой были выполнены с двойной точностью. По этой причине целое число (или что-либо еще) никогда не было неявно преобразовано в float, но только в double. Float также не может быть типом аргумента функции: вам нужно было передать указатель на float, если вы действительно, действительно, действительно хотели избежать преобразования в double. По этой причине функции
int x(float a)
{ ... }
и
int y(a)
float a;
{ ... }
имеют различные соглашения о вызовах. Первый получает аргумент float, второй (теперь уже не разрешимый как синтаксис) получает двойной аргумент.
одинарной точности с плавающей точкой арифметические и функциональные аргументы были введены только с ANSI C. Kernighan / Ritchie невиновен.
теперь с новым доступным single float выражения (single float ранее был только форматом хранения), также должны были быть преобразования нового типа. Независимо от того, что команда ANSI C выбрала здесь (и я был бы в недоумении для лучшего выбора), это не вина K&R.
Q1: может ли float представлять все значения int?
IEE754 может представлять все целые числа точно как поплавки, примерно до 223, как указано в этой ответ.
Q2: почему бы не повысить как int, так и float до double?
правила в стандарте для этих преобразований являются незначительными модификациями правил в K&R: модификации учитывают добавленные типы и правила сохранения значений. явная лицензия была добавлена для выполнения вычислений в "более широком" типе, чем абсолютно необходимо, так как это иногда может производить меньший и более быстрый код, не говоря уже о правильном ответе чаще. вычисления также могут выполняться в" более узком " типе по правилу as if, если получен тот же конечный результат. Явное приведение всегда можно использовать для получения значения в желаемом типе.
выполнение вычисления в более широком типе означают, что задано float f1; и float f2;, f1 + f2 может быть вычислена в double точности. А это значит, что данный int i; и float f;, i == f может быть вычислена в double точности. Но не требуется вычислять i == f с двойной точностью, как указано в комментарии hvd.
также стандарт C говорит так. Они известны как обычные арифметические преобразования . Следующее описание взято прямо из ANSI C норматив.
...если один из операндов имеет тип float, другой операнд преобразуется в тип float .
источник и вы можете увидеть его в ref тоже.
соответствующая ссылка, это ответ. Более аналитический источник -здесь.
вот еще один способ объяснить это: обычные арифметические преобразования неявно выполняются для приведения их значений в общей тип. Компилятор сначала выполняет целочисленное продвижение, если операнды все еще имеют разные типы, то они преобразуются в тип, который отображается выше в следующей иерархии:
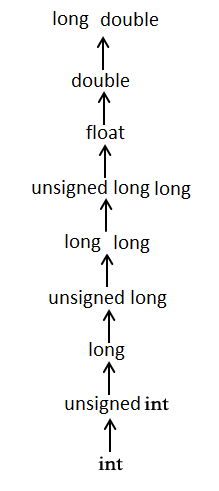
при создании языка программирования некоторые решения принимаются интуитивно.
например, почему бы не преобразовать int + float в int+int вместо float+float или double+double? Зачем вызывать int - >float продвижение, если оно содержит то же самое о битах? Почему бы не вызвать float - >int a promotion?
Если вы полагаетесь на неявные преобразования типов, вы должны знать, как они работают, иначе просто конвертируйте вручную.
какой язык мог быть разработан без каких-либо автоматическое преобразование типов вообще. И не каждое решение на этапе проектирования могло быть принято логически с хорошей причиной.
JavaScript с его утиной типизацией имеет еще более неясные решения под капотом. Разработка абсолютно логического языка невозможна,я думаю, что это относится к теореме Геделя о неполноте. Вы должны уравновесить логику, интуицию, практику и идеалы.
вопрос в том, почему: потому что это быстро, легко объяснить, легко скомпилировать, и все это были очень важные причины в то время, когда был разработан язык C.
У вас могло быть другое правило: для каждого сравнения арифметических значений результатом является сравнение фактических числовых значений. Это было бы где-то между тривиальным, если одно из сравниваемых выражений является константой, одной дополнительной инструкцией при сравнении signed и unsigned int и довольно сложно, если вы сравниваете long long и double и хотите получить правильные результаты, когда long long не может быть представлен как double. (0u
в Swift, проблема легко решается путем запрета операций между различными типами.
правила написаны для 16-битных ints (наименьший необходимый размер). Ваш компилятор с 32-битными вставками, безусловно, преобразует обе стороны в double. В современном оборудовании нет поплавковых регистров, так что это и для преобразования в double. Теперь, если у вас есть 64 бит ints, я не слишком уверен, что он делает. длинный двойной был бы уместен (обычно 80 бит, но это даже не стандарт).
