Почему random () * random () отличается от random () * * 2?
есть ли разница между random() * random() и random() ** 2? random() возвращает значение от 0 до 1 с равномерным распределением.
при тестировании обеих версий случайных квадратных чисел я заметил небольшую разницу. Я создал 100000 случайных квадратных чисел и подсчитал, сколько чисел находится в каждом интервале 0.01 (0.00-0.01, 0.01-0.02,...). Похоже, что эти версии генерации случайных чисел в квадрате отличаются.
квадратура случайное число вместо умножения двух случайных чисел вы используете случайное число, но я думаю, что распределение должно оставаться прежним. Разве есть разница? Если нет, то почему мой тест показывает разницу?
я генерирую два случайных бинарных распределения для random() * random() и random() ** 2 вот так:
from random import random
lst = [0 for i in range(100)]
lst2, lst3 = list(lst), list(lst)
#create two random distributions for random() * random()
for i in range(100000):
lst[int(100 * random() * random())] += 1
for i in range(100000):
lst2[int(100 * random() * random())] += 1
for i in range(100000):
lst3[int(100 * random() ** 2)] += 1
что дает
>>> lst
[
5626, 4139, 3705, 3348, 3085, 2933, 2725, 2539, 2449, 2413,
2259, 2179, 2116, 2062, 1961, 1827, 1754, 1743, 1719, 1753,
1522, 1543, 1513, 1361, 1372, 1290, 1336, 1274, 1219, 1178,
1139, 1147, 1109, 1163, 1060, 1022, 1007, 952, 984, 957,
906, 900, 843, 883, 802, 801, 710, 752, 705, 729,
654, 668, 628, 633, 615, 600, 566, 551, 532, 541,
511, 493, 465, 503, 450, 394, 405, 405, 404, 332,
369, 369, 332, 316, 272, 284, 315, 257, 224, 230,
221, 175, 209, 188, 162, 156, 159, 114, 131, 124,
96, 94, 80, 73, 54, 45, 43, 23, 18, 3
]
>>> lst2
[
5548, 4218, 3604, 3237, 3082, 2921, 2872, 2570, 2479, 2392,
2296, 2205, 2113, 1990, 1901, 1814, 1801, 1714, 1660, 1591,
1631, 1523, 1491, 1505, 1385, 1329, 1275, 1308, 1324, 1207,
1209, 1208, 1117, 1136, 1015, 1080, 1001, 993, 958, 948,
903, 843, 843, 849, 801, 799, 748, 729, 705, 660,
701, 689, 676, 656, 632, 581, 564, 537, 517, 525,
483, 478, 473, 494, 457, 422, 412, 390, 384, 352,
350, 323, 322, 308, 304, 275, 272, 256, 246, 265,
227, 204, 171, 191, 191, 136, 145, 136, 108, 117,
93, 83, 74, 77, 55, 38, 32, 25, 21, 1
]
>>> lst3
[
10047, 4198, 3214, 2696, 2369, 2117, 2010, 1869, 1752, 1653,
1552, 1416, 1405, 1377, 1328, 1293, 1252, 1245, 1121, 1146,
1047, 1051, 1123, 1100, 951, 948, 967, 933, 939, 925,
940, 893, 929, 874, 824, 843, 868, 800, 844, 822,
746, 733, 808, 734, 740, 682, 713, 681, 675, 686,
689, 730, 707, 677, 645, 661, 645, 651, 649, 672,
679, 593, 585, 622, 611, 636, 543, 571, 594, 593,
629, 624, 593, 567, 584, 585, 610, 549, 553, 574,
547, 583, 582, 553, 536, 512, 498, 562, 536, 523,
553, 485, 503, 502, 518, 554, 485, 482, 470, 516
]
ожидаемая случайная ошибка-это разница в первых двух:
[
78, 79, 101, 111, 3, 12, 147, 31, 30, 21,
37, 26, 3, 72, 60, 13, 47, 29, 59, 162,
109, 20, 22, 144, 13, 39, 61, 34, 105, 29,
70, 61, 8, 27, 45, 58, 6, 41, 26, 9,
3, 57, 0, 34, 1, 2, 38, 23, 0, 69,
47, 21, 48, 23, 17, 19, 2, 14, 15, 16,
28, 15, 8, 9, 7, 28, 7, 15, 20, 20,
19, 46, 10, 8, 32, 9, 43, 1, 22, 35,
6, 29, 38, 3, 29, 20, 14, 22, 23, 7,
3, 11, 6, 4, 1, 7, 11, 2, 3, 2
]
но разница между первым и третьим намного больше, намекая на то, что распределения разные:
[
4421, 59, 491, 652, 716, 816, 715, 670, 697, 760,
707, 763, 711, 685, 633, 534, 502, 498, 598, 607,
475, 492, 390, 261, 421, 342, 369, 341, 280, 253,
199, 254, 180, 289, 236, 179, 139, 152, 140, 135,
160, 167, 35, 149, 62, 119, 3, 71, 30, 43,
35, 62, 79, 44, 30, 61, 79, 100, 117, 131,
168, 100, 120, 119, 161, 242, 138, 166, 190, 261,
260, 255, 261, 251, 312, 301, 295, 292, 329, 344,
326, 408, 373, 365, 374, 356, 339, 448, 405, 399,
457, 391, 423, 429, 464, 509, 442, 459, 452, 513
]
2 ответов
вот несколько сюжетов:
все возможности random() * random():

ось x-это одна случайная величина, увеличивающаяся вправо, а ось y-другая, увеличивающаяся вверх.
вы можете видеть, что если низкая, то и результат будет низким, и оба должны быть выше, чтобы получить высокий результат.
когда единственным решающим фактором является одна ось, как в random() ** 2 случае, вы get

в этом случае гораздо более вероятно получить очень темное (большое) значение, так как весь верх темный, а не только угол.
когда вы делаете оба линеаризованных, с random() * random() сверху:


вы видите, что распределения действительно разные.
код:
import numpy
import matplotlib
from matplotlib import pyplot
import matplotlib.cm
def make_fig(name, data):
figure = matplotlib.pyplot.figure()
print(data.shape)
figure.set_size_inches(data.shape[1]//100, data.shape[0]//100)
axes = matplotlib.pyplot.Axes(figure, [0, 0, 1, 1])
axes.set_axis_off()
figure.add_axes(axes)
axes.imshow(data, origin="lower", cmap=matplotlib.cm.Greys, aspect="auto")
figure.savefig(name, dpi=200)
xs, ys = numpy.mgrid[:1000, :1000]
two_random = xs * ys
make_fig("two_random.png", two_random)
two_random_flat = two_random.flatten()
two_random_flat.sort()
two_random_flat = two_random_flat[::1000]
make_fig("two_random_1D.png", numpy.tile(two_random_flat, (100, 1)))
one_random = xs * xs
make_fig("one_random.png", one_random)
one_random_flat = one_random.flatten()
one_random_flat.sort()
one_random_flat = one_random_flat[::1000]
make_fig("one_random_1D.png", numpy.tile(one_random_flat, (100, 1)))
вы также можете подойти к этому математически. Вероятность получения значения меньше x С 0 ≤ x ≤ 1 и
на random()²:
√x
как вероятность случайного значения ниже, чем x вероятность того, что random()² < x.
на random() · random():
учитывая, что первая случайная величина r и второй R, мы можем найти вероятность того, что Rr < x фиксированный R:
P(Rr < x)
= P(r < x/R)
= 1 if x > R (and so x/R > 1)
or
= x/R otherwise
Итак, мы хотим
∫ P(Rr < x) dR from R=0 to R=1
= ∫ 1 dR from R=0 to R=x
+ ∫ x/R dR from R=x to R=1
= x(1 - ln R)
как мы видим, √x ≠ x(1 - ln R).
эти распределения отображаются как:
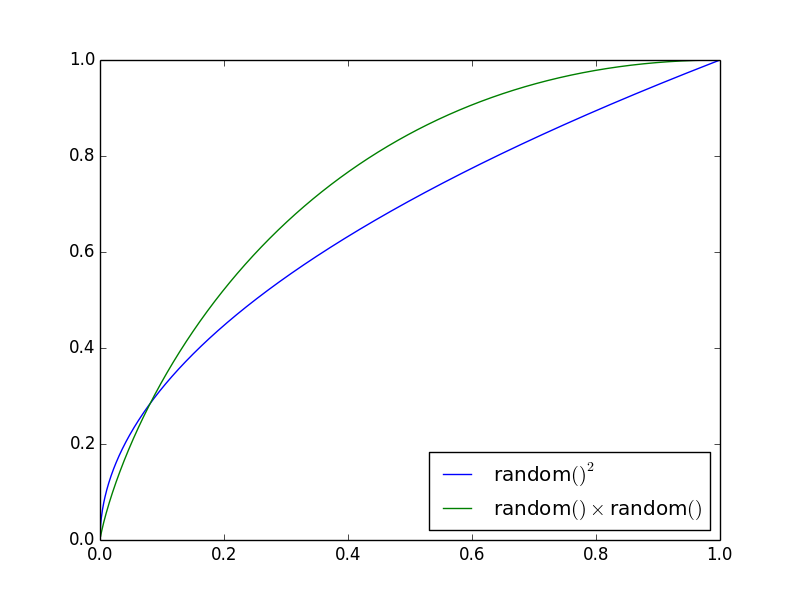
ось y дает вероятность того, что линия (random()² или random() · random()) меньше оси Х.
мы видим, что для random() · random() вероятность больших чисел значительно меньше.
функции плотности
я думаю, что самое показательное-дифференцировать (½x ^ -½ и - ln x) и построить плотность вероятности функции:
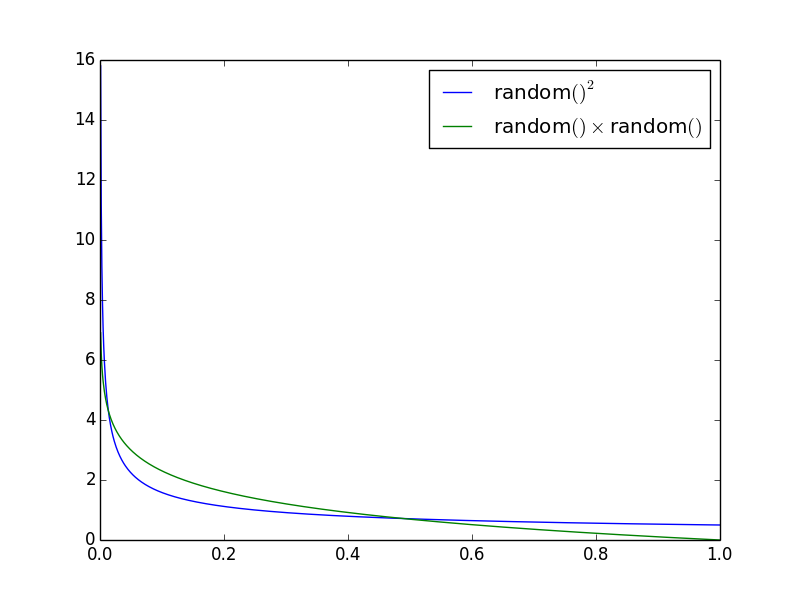
это показывает вероятность каждого x в относительном выражении. Так что вероятность того, что x большой (> 0.5) примерно в два раза для random()² вариант.
давайте несколько упростим задачу. Подумайте о бросании двух кубиков и умножении результата на бросание одного кубика и возведение его в квадрат. В первом случае у вас есть 1 шанс из 36 бросить двойной 1, поэтому 1 шанс из 36 продукт равен 1. С другой стороны, второй случай, очевидно, имеет 1 шанс из 6, что квадрат равен 1. То же самое относится и к двойному 6, поэтому крайности гораздо более вероятны при возведении в квадрат.
то же самое следует, когда вы используете случайные поплавки: вы гораздо менее вероятно получить два случайных значения в экстремумах, чем получить одно значение, поэтому очень маленькие или очень большие значения будут появляться гораздо чаще при возведении в квадрат, чем при умножении двух независимых значений.
