Почему результаты свертки имеют разную длину при выполнении во временной области vs в частотной области?
Я не эксперт DSP, но я понимаю, что есть два способа, которыми я могу применить дискретный фильтр временной области к дискретной форме волны временной области. Первый состоит в том, чтобы свернуть их во временной области, а второй-взять БПФ обоих, умножить оба сложных спектра и принять IFFT результата. Одним из ключевых отличий этих методов является то, что второй подход подвержен круговой свертке.
в качестве примера, если фильтр и сигналы имеют длину N точек, то первый подход (т. е. свертка) дает результат длиной N+N-1 точек, где первая половина этого ответа-заполнение фильтра, а вторая половина-опорожнение фильтра. Чтобы получить стационарный ответ, фильтр должен иметь меньше точек, чем форма волны для фильтрации.
продолжая этот пример со вторым подходом и предполагая, что дискретные данные формы волны во временной области являются реальными (не сложными), БПФ фильтра и формы волны производят БПФ N очки длинные. Умножение обоих спектров в результате приводит к результату во временной области также N точек. Здесь ответ, где фильтр заполняет и опустошает, перекрывает друг друга во временной области, и нет стационарного ответа. Это эффект круговой свертки. Чтобы избежать этого, как правило, размер фильтра будет меньше, чем размер формы волны, и оба будут нулевыми, чтобы позволить пространству для свертки частоты расширяться во времени после IFFT продукта двух спектры.
мой вопрос в том, что я часто вижу работу в литературе от известных экспертов/компаний, где у них есть дискретная (реальная) форма волны во временной области (N точек), они FFT, умножают ее на некоторый фильтр (также N точек) и IFFT результат для последующей обработки. Мое наивное мышление заключается в том, что этот результат не должен содержать стационарного ответа и, следовательно, должен содержать артефакты из заполнения/опорожнения фильтра, что приведет к ошибкам в интерпретации полученных данных, но я должно быть, чего-то не хватает. При каких обстоятельствах это может быть правильный подход?
любое понимание было бы очень признательно
4 ответов
основная проблема заключается не в нулевом заполнении против предполагаемой периодичности, а в том, что анализ Фурье разлагает сигнал на синусоидальные волны, которые на самом базовом уровне считаются бесконечными по протяженности. оба подхода верны в том, что IFFT, используя полный БПФ, вернет точную форму входного сигнала и оба подхода неверны в том, что использование менее полного спектра может привести к эффектам на краях (которые обычно расширяют несколько диапазон волн.) Единственная разница заключается в деталях того, что вы предполагаете, заполняет остальную часть бесконечности, а не в том, делаете ли вы предположение.
вернемся к вашему первому абзацу: обычно в DSP самая большая проблема, с которой я сталкиваюсь с FFS, заключается в том, что они не являются причинными, и по этой причине я часто предпочитаю оставаться во временной области, используя, например, фильтры FIR и IIR.
обновление:
в постановке вопроса OP правильно указывает некоторые из проблем, которые могут возникнуть при использовании FFTs для фильтрации сигналов, например, краевые эффекты, которые могут быть особенно проблематичными при выполнении свертки, сопоставимой по длине (во временной области) с дискретизированной формой волны. Важно отметить, что не вся фильтрация выполняется с помощью FFTs, и в статье, цитируемой OP, они не используют фильтры FFT, и проблемы, которые возникли бы с реализацией фильтра FFT, не возникают с использованием их подходи!--14-->.
рассмотрим, например, фильтр, который реализует простое среднее значение по 128 точкам выборки, используя две разные реализации.
FFT: в подходе FFT / свертки будет иметь образец, скажем, 256 точек и свернуть это с wfm, который является постоянным для первой половины и переходит к нулю во второй половине. Здесь вопрос (даже после нескольких циклов), что определяет значение первой точки результат? БПФ предполагает, что wfm является круговым (т. е. бесконечно периодическим), поэтому: первая точка результата определяется последние 127 (т. е. будущие) образцы wfm (пропуск через середину wfm) или на 127 нулей, если вы нуль-колодки. Ни правильно.
FIR: другой подход-реализовать среднее значение с помощью FIR-фильтра. Например, здесь можно использовать среднее значение значений в очереди FIFO 128 регистров. То есть, по мере поступления каждой точки выборки 1) поместите ее в очередь, 2) Удалите самый старый элемент, 3) усредните все 128 элементов, оставшихся в очереди; и это ваш результат для этой точки выборки. Этот подход работает непрерывно, обрабатывая одну точку за раз и возвращая отфильтрованный Результат после каждой выборки, и не имеет никаких проблем, возникающих из БПФ, поскольку он применяется к конечным частям выборки. Каждый результат - это только среднее значение текущей выборки и 127 выборок, которые были получены ранее он.
документ, который цитирует OP, использует подход, гораздо более похожий на FIR-фильтр, чем на FFT-фильтр (обратите внимание, что фильтр в бумаге сложнее, и вся статья в основном является анализом этого фильтра.) См., например, эта бесплатная книга который описывает, как анализировать и применять различные фильтры, а также отметить, что подход Лапласа к анализу фильтров FIR и IIR довольно похож на то, что найдено в приведенном бумага.
вот пример свертки без нулевого заполнения для DFT (круговой свертки) против линейной свертки. Это свертка последовательности длины M=32 с последовательностью длины L=128 (с использованием Numpy/Matplotlib):
f = rand(32); g = rand(128)
h1 = convolve(f, g)
h2 = real(ifft(fft(f, 128)*fft(g)))
plot(h1); plot(h2,'r')
grid()
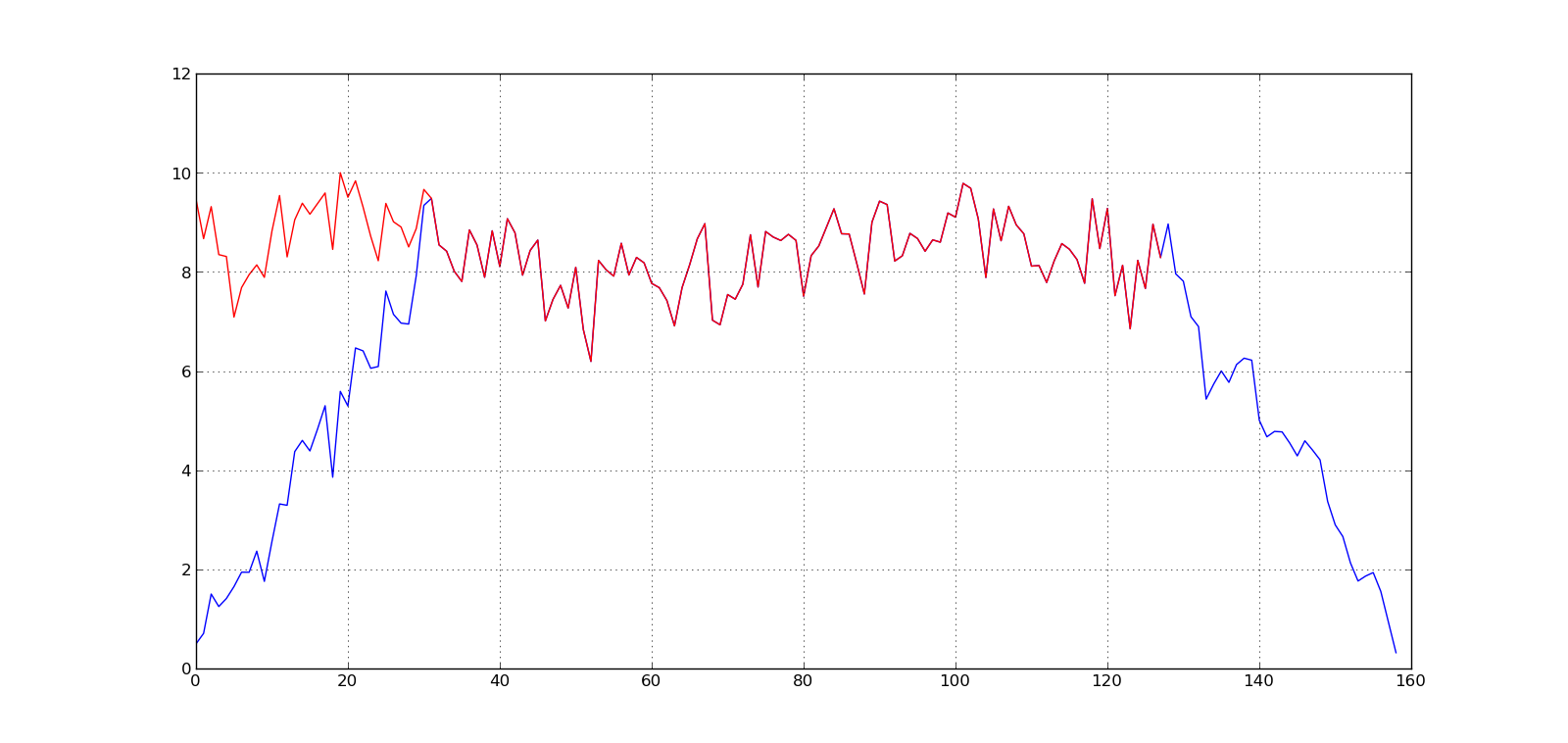Первые точки M-1 отличаются, и они короткие на M-1, так как они не были нулевыми. Эти различия являются проблемой при выполнении свертки блоков, но такие методы, как перекрытие и сохранение или перекрытие и добавление, используются для преодолеть эту проблему. В противном случае, если вы просто вычисляете одноразовую операцию фильтрации, действительный результат начнется с индекса M-1 и закончится индексом L-1 с длиной L-M+1.
Что касается приведенной статьи, я посмотрел на их код MATLAB в приложении A. Я думаю, что они допустили ошибку в применении передаточной функции Hfinal к отрицательным частотам без ее первого сопряжения. В противном случае вы можете видеть на своих графиках, что тактовый джиттер является периодическим сигналом, поэтому используйте круговой свертка хороша для стационарного анализа.
Edit: что касается сопряжения передаточной функции, PLLs имеют вещественную импульсную характеристику, и каждый вещественный сигнал имеет сопряженный симметричный спектр. В коде вы можете видеть, что они просто используют Hfinal[N-i], чтобы получить отрицательные частоты, не принимая конъюгата. Я построил их передаточную функцию от -50 МГц до 50 МГц:
N = 150000 # number of samples. Need >50k to get a good spectrum.
res = 100e6/N # resolution of single freq point
f = res * arange(-N/2, N/2) # set the frequency sweep [-50MHz,50MHz), N points
s = 2j*pi*f # set the xfer function to complex radians
f1 = 22e6 # define 3dB corner frequency for H1
zeta1 = 0.54 # define peaking for H1
f2 = 7e6 # define 3dB corner frequency for H2
zeta2 = 0.54 # define peaking for H2
f3 = 1.0e6 # define 3dB corner frequency for H3
# w1 = natural frequency
w1 = 2*pi*f1/((1 + 2*zeta1**2 + ((1 + 2*zeta1**2)**2 + 1)**0.5)**0.5)
# H1 transfer function
H1 = ((2*zeta1*w1*s + w1**2)/(s**2 + 2*zeta1*w1*s + w1**2))
# w2 = natural frequency
w2 = 2*pi*f2/((1 + 2*zeta2**2 + ((1 + 2*zeta2**2)**2 + 1)**0.5)**0.5)
# H2 transfer function
H2 = ((2*zeta2*w2*s + w2**2)/(s**2 + 2*zeta2*w2*s + w2**2))
w3 = 2*pi*f3 # w3 = 3dB point for a single pole high pass function.
H3 = s/(s+w3) # the H3 xfer function is a high pass
Ht = 2*(H1-H2)*H3 # Final transfer based on the difference functions
subplot(311); plot(f, abs(Ht)); ylabel("abs")
subplot(312); plot(f, real(Ht)); ylabel("real")
subplot(313); plot(f, imag(Ht)); ylabel("imag")
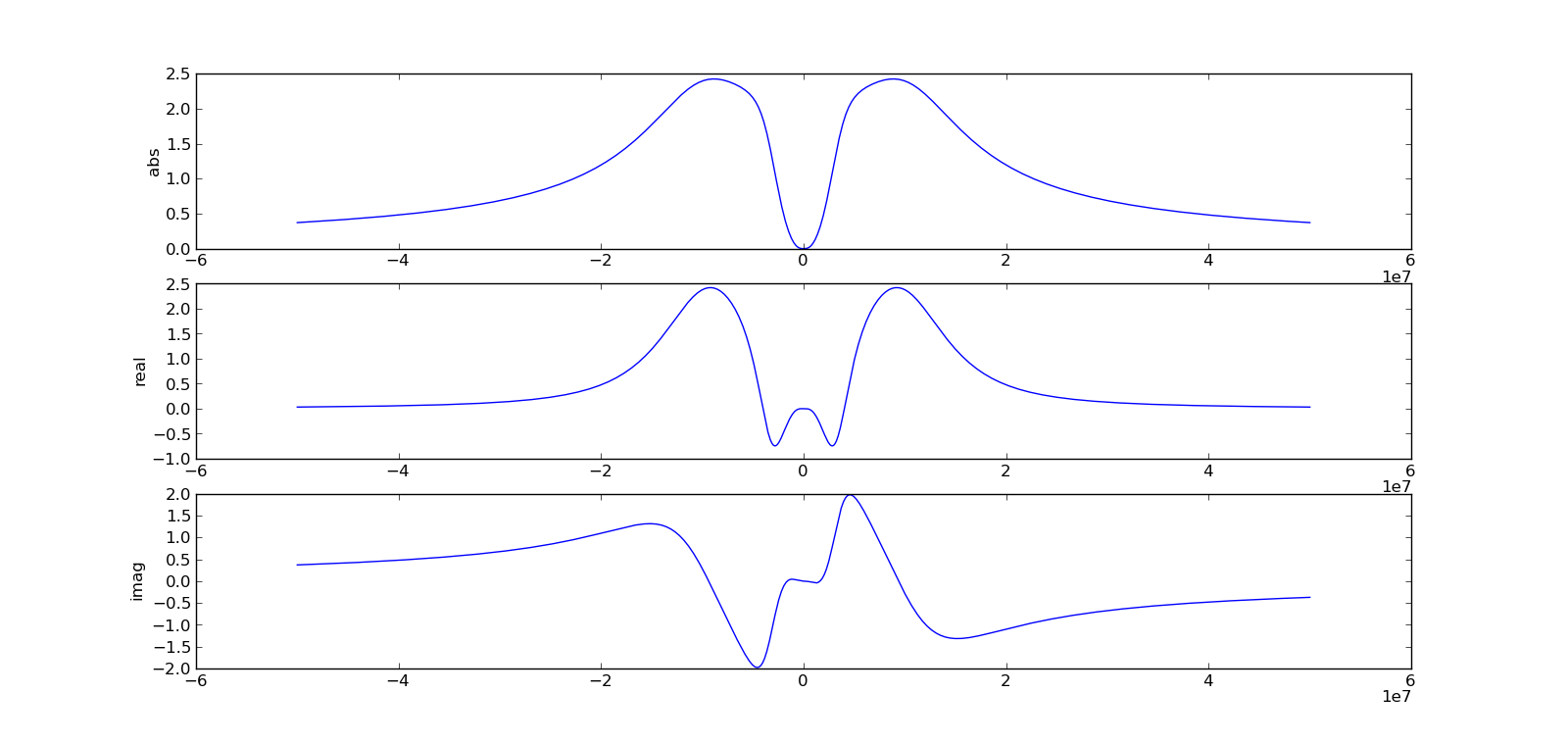
Как вы можете видеть, реальный компонент имеет четную симметрию, а мнимая - нечетную. В своем коде они рассчитаны только положительных частот для loglog участок (достаточно разумного). Однако для вычисления обратного преобразования они использовали значения положительных частот для отрицательных частот путем индексации Hfinal[N-i], но забыли его сопрягать.
хотя будут артефакты от предположения, что прямоугольное окно данных является периодическим при ширине апертуры FFT, что является одной из интерпретаций того, что делает круговая свертка без достаточного заполнения нуля, различия могут быть или не быть достаточно большими, чтобы затопить анализ данных, о котором идет речь.
Я могу пролить свет на причину, по которой "окно" применяется до применения БПФ.
Как уже указывалось, БПФ предполагает, что у нас есть бесконечный сигнал. Когда мы берем выборку за конечное время T, это математически эквивалентно умножению сигнала на прямоугольную функцию.
умножение во временной области становится сверткой в частотной области. Частотная характеристика прямоугольника-это функция синхронизации, т. е. sin (x)/x. X в числитель-это Кикер, потому что он замирает O(1/N).
Если у вас есть частотные компоненты, которые точно кратны 1/T, это не имеет значения, поскольку функция синхронизации равна нулю во всех точках, кроме той частоты, где она равна 1.
однако, если у вас есть синус, который падает между 2 точками, вы увидите функцию синхронизации, выбранную на частотной точке. Он lloks как увеличенная версия функции синхронизации и сигналы "призрака", вызванные сверткой, умирают с 1 / N или 6db / octave. Если у вас есть сигнал 60db выше уровня шума, вы не увидите шум для 1000 частот слева и справа от вашего основного сигнала, он будет завален "юбками" функции синхронизации.
Если вы используете другое окно времени, то вы получаете другую частотную характеристику, Косинус например умирает вниз с 1 / x^2, специализированные окна для различных измерений. Окно Hanning часто используется в качестве окна общего назначения.
точка что прямоугольное окно, используемое без применения какой-либо" оконной функции", создает гораздо худшие артефакты, чем хорошо выбранное окно. Я. e "искажая" временные выборки, мы получаем гораздо лучшую картину в частотной области, которая ближе напоминает "реальность" или, скорее, "реальность", которую мы ожидаем и хотим видеть.