Почему слияние сортирует наихудшее время выполнения o (n log n)?

на Сортировка Слиянием использовать Разделяй и властвуй подход к решению проблемы сортировки. Во-первых, он делит вход пополам с помощью рекурсии. После разделения он сортирует половинки и объединяет их в один отсортированный вывод. См. рисунок

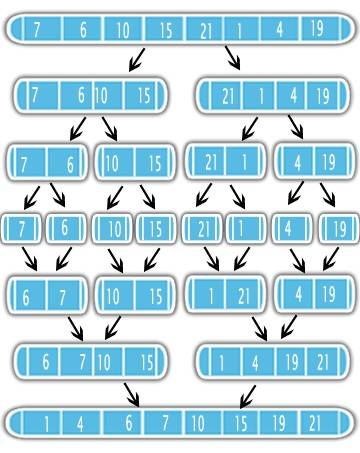
это означает, что лучше сначала отсортировать половину вашей проблемы и выполнить простую подпрограмму слияния. Поэтому важно знать сложность подпрограммы слияния и сколько раз она будет выполняться вызывается рекурсия.

псевдо-код сортировка слиянием - Это очень просто.

# C = output [length = N]
# A 1st sorted half [N/2]
# B 2nd sorted half [N/2]
i = j = 1
for k = 1 to n
    if A[i] < B[j]
        C[k] = A[i]
        i++
    else
        C[k] = B[j]
        j++

легко видеть, что в каждом цикле у вас будет 4 операции: k++, i++ или j++ на if оператор и атрибуция C = A / B. Таким образом, у вас будет меньше или равно 4N + 2 операций, дающих O (N) сложности. Ради доказательства 4N + 2 будет рассматриваться как 6N, так как это верно для N = 1 (4N +2 ).

предположим, у вас есть вход с N элементы и предположить N сила 2. На каждом уровне у вас в два раза больше подзадач с входом с половиной элементов от предыдущего входа. Это означает, что на уровне j = 0, 1, 2, ..., lgN там будет 2^j подзадачи с вводом длины N / 2^j. Количество операций на каждом уровне j будет меньше или равна

2^j * 6 (N / 2^j) = 6N

заметьте, что это не имеет значения, на каком уровне у вас всегда будет меньше или равно 6N операций.

поскольку есть уровни lgN + 1, сложность будет

O (6N * (lgN + 1)) = O (6N*lgN + 6N) = O (n lgN)

ссылки:

• Coursera алгоритмы курса: проектирование и Анализ, Часть 1

Это потому, что будь то худший или средний случай, сортировка слияния просто делит массив на две половины на каждом этапе, который дает ему компонент lg(n), а другой компонент N исходит из его сравнений, которые сделаны на каждом этапе. Таким образом, объединение становится почти O (nlg n). Независимо от того, является ли это средним случаем или худшим случаем, фактор lg(n) всегда присутствует. Коэффициент покоя N зависит от сделанных сравнений, которые происходят из сравнений, сделанных в обоих случаях. Теперь худший случай-тот, в котором N сравнение происходит на входе N на каждом этапе. Таким образом, он становится O(nlg n).

после разбиения массива на стадии, когда у вас есть отдельные элементы, т. е. назвать их подсписки,

• на каждом этапе мы сравниваем элементы каждого подсписка с его смежным подсписком. Например, [повторное использование изображения @Davi ]

  

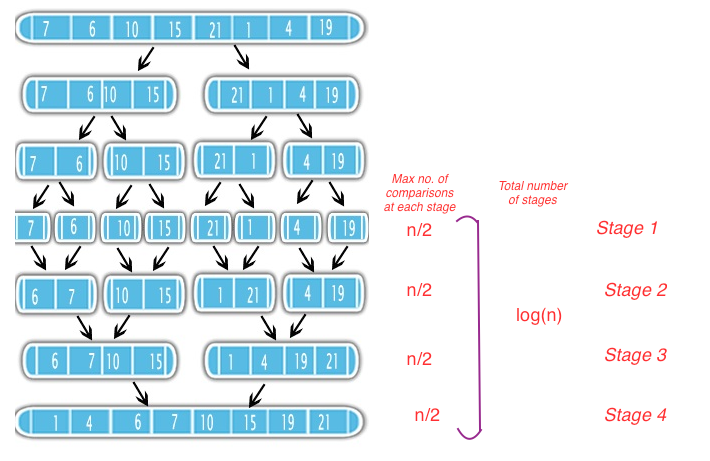
  1. на этапе-1 каждый элемент сравнивается с соседним, поэтому N / 2 сравнения.
  2. на этапе-2 каждый элемент подсписка сравнивается с соседним подсписком, поскольку каждый подсписок отсортирован, это означает, что максимальное число сравнений между двумя подсписями равно n/2
  3. как вы заметили, общее количество этапов будет log(n) base 2 Таким образом, общая сложность будет == (максимальное количество сравнения на каждом этапе * количество этапов) = = O ((n/2)*log(n)) ==> O (nlog (n))

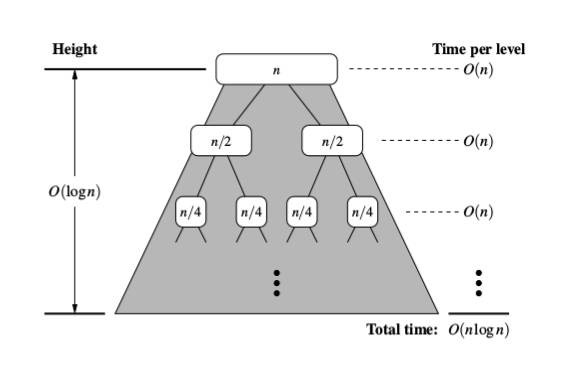
алгоритм MergeSort делает три шага:

1. разделить шаг вычисляет среднее положение суб-массива и занимает постоянное время O(1).
2. победить шаг рекурсивно сортировать два суб массивов приблизительно n / 2 элементов каждый.
3. комбината шаг объединяет в общей сложности n элементов на каждом проходе, требующем не более n сравнений, поэтому он принимает O(n).

алгоритм требует приблизительно logn проходит для сортировки массив из n элементов и поэтому общая временная сложность nlogn.

многие другие ответы отличные, но я не видел никакого упоминания о высота и глубина связанные с примерами" дерева слияния-сортировки". Вот еще один способ подойти к вопросу с большим вниманием к дереву. Вот еще одно изображение, чтобы помочь объяснить:

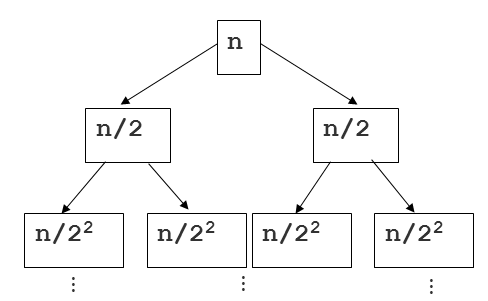
просто резюме: как указывали другие ответы, мы знаем, что работа слияния двух отсортированных срезов последовательности выполняется в линейное время (вспомогательная функция слияния то, что мы вызываем из основной функции сортировки).
Теперь, глядя на это дерево, где мы можем думать о каждом потомке корня (кроме корня) как о рекурсивном вызове функции сортировки, давайте попробуем оценить, сколько времени мы тратим на каждый узел... Поскольку нарезка последовательности и слияние (оба вместе) занимают линейное время, время работы любого узла линейно относительно длины последовательности На этом узле.

вот где глубина дерево. Если n - общий размер исходной последовательности, размер последовательности на любом узле равен n / 2^Я, где я-глубина. Это показано на рисунке выше. Положив это вместе с линейным объемом работы для каждого среза, мы имеем время выполнения O (n/2^Я) для каждого узла в дереве. Теперь мы просто должны суммировать это для n узлов. Один из способов сделать это-признать, что есть 2^Я узлы на каждом уровне глубины в дереве. Так для любого уровня, мы имеем O (2^Я * n / 2^Я), который является O(n), потому что мы можем отменить 2^Яs! Если каждая глубина равна O (n), мы просто должны умножить это на высота этого двоичного дерева, которое является logn. Ответ: O (nlogn)

ссылки: структуры данных и алгоритмы в Python

алгоритм слияния-сортировка сортирует последовательность s размера n в O (N log n) время, предполагая, что два элемента S можно сравнить в O (1) времени.

рекурсивное дерево будет иметь глубину log(N), и на каждом уровне в этом дереве вы будете делать комбинированный N работа для слияния двух отсортированных массивов.

слияние сортированных массивов

объединить два отсортированных массива A[1,5] и B[3,4] вы просто повторяете оба, начиная с начала, выбирая самый низкий элемент между двумя массивами и увеличивая указатель для этого массива. Вы закончите, когда оба указателя достигнут конца их соответствующих матрицы.

[1,5] [3,4]  --> []
 ^     ^

[1,5] [3,4]  --> [1]
   ^   ^

[1,5] [3,4]  --> [1,3]
   ^     ^

[1,5] [3,4]  --> [1,3,4]
   ^      x

[1,5] [3,4]  --> [1,3,4,5]
    x     x

Runtime = O(A + B)

сортировка слиянием иллюстрации

ваш рекурсивный стек вызовов будет выглядеть следующим образом. Работа начинается в нижних листовых узлах и пузырится вверх.

beginning with [1,5,3,4], N = 4, depth k = log(4) = 2

  [1,5]    [3,4]     depth = k-1 (2^1 nodes) * (N/2^1 values to merge per node) == N
[1]  [5]  [3]  [4]   depth = k   (2^2 nodes) * (N/2^2 values to merge per node) == N

таким образом вы делаете N работы на каждом из k уровни в дереве, где k = log(N)

N * k = N * log(N)