Поиск кратчайшего пути на графике с дополнительными ограничениями
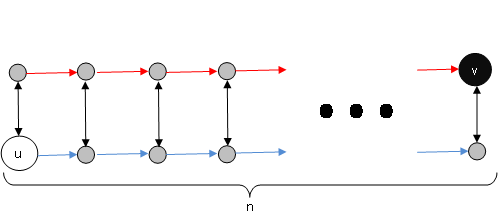
У меня есть график с 2n вершин, где каждое ребро имеет определенную длину. Похоже на**
**.
Я пытаюсь найти длину кратчайшего пути из u to v (наименьшая сумма длин ребер), с 2 дополнительными ограничениями:
- количество синих ребер, которые содержит путь, совпадает с количеством красных ребер.
- в количество черных ребер, содержащихся в пути, не превышает p.
Я придумал алгоритм экспоненциального времени, который, я думаю, будет работать. Он повторяет все двоичные комбинации длины n-1 которые представляют путь, начинающийся с u следующим образом:
- 0 синий край
- 1 красный края
- есть черный край всякий раз
- комбинация начинается с 1. Первый край (от u) является первым черным слева.
- комбинация заканчивается 0. Затем последний край (до v) является последним черным справа.
- соседние цифры различны. Это означает, что мы перешли от синего края к красному краю (или наоборот), поэтому есть черный между.
этот алгоритм проигнорирует пути, которые не соответствуют 2 требованиям, упомянутым ранее, и вычислит длину для тех, которые это делают, а затем найдет самый короткий. Однако делать это таким образом, вероятно, будет ужасно медленно, и я ищу несколько советов, чтобы придумать более быстрый алгоритм. Я подозреваю, что это можно достичь с помощью динамического программирования, но я не знаю с чего начать. Любая помощь будет очень ценится. Спасибо.
3 ответов
Edit: как-то я посмотрел на фразу "найти кратчайший путь" в вопросе и проигнорировал "длину" фразы, где исходный вопрос позже прояснил намерение. Поэтому оба моих ответа ниже хранят много дополнительных данных, чтобы легко отследить правильный путь, как только вы вычислите его длину. Если вам не нужно возвращаться после вычисления длины, моя грубая версия может изменить свое первое измерение С N на 2 и просто сохранить один нечетный J и один четный J, перезаписывая что-либо старше. Моя более быстрая версия может отбросить всю сложность управления взаимодействиями J,R, а также просто сохранить внешний уровень как [0..1][0..H] ничто из этого не сильно меняет время, но оно сильно меняет хранилище.
обратите внимание, что N должно быть нечетным, представим это как N=2H+1. (P также должно быть нечетным. Просто уменьшите P, если задано четное P. Но отклоните вход, если N четное.)
стоимость хранения с использованием 3 реальных координат и одной подразумеваемой координаты:
J = столбец от 0 до n
R = количество красных ребер от 0 до H
B = количество черных краев от 0 до P
S = сторона нечетная или четная (S просто B%1)
мы будем вычислять / хранить стоимость[J] [R] [B] как самый дешевый способ достичь столбца J, используя ровно R красных краев и ровно B черных краев. (Мы также использовали J-R синие края, но этот факт излишен).
Для удобства пишите в cost напрямую, но прочитайте его через accessor c (j,r,b), который возвращает BIG when r<0 || b<0 и возвращает стоимость[j][r][b] в противном случае.
тогда самый внутренний шаг просто:
If (S)
cost[J+1][R][B] = red[J]+min( c(J,R-1,B), c(J,R-1,B-1)+black[J] );
else
cost[J+1][R][B] = blue[J]+min( c(J,R,B), c(J,R,B-1)+black[J] );
инициализировать cost[0] [0] [0] до нуля и для супер сырой версии инициализировать все остальные cost[0] [R] [B] до BIG.
Вы могли бы супер грубо просто цикл через увеличение последовательности J и любой последовательности R, B вам нравится вычислять все это.
в конце концов, мы можем найти ответ как:
min( min(cost[N][H][all odd]), black[N]+min(cost[N][H][all even]) )
но половина значений R на самом деле не частью проблемы. В первом тайме любой R>J невозможны и во втором тайме любые R<J+H-N бесполезны. Вы можете легко избежать их вычисления. С немного более умной функцией доступа вы можете избежать использования позиций, которые вы никогда не вычисляли в граничных случаях тех, которые вам нужно вычислить.
если любая новая цена[J][R][B] не меньше, чем стоимость тех же J, R и S, но ниже B, что новая стоимость бесполезных данных. Если бы последним тусклым пятном структуры была карта, а не массив, мы могли бы легко вычислить в последовательности, которая отбрасывает эти бесполезные данные как из пространства хранения, так и из времени. Но это уменьшенное время затем умножается на журнал среднего размера (до P) этих карт. Так что, вероятно, победа в среднем случае, но, скорее всего, проигрыш в худшем случае.
дайте немного подумать о типе данных, необходимых для стоимости и значение, необходимое для большого. Если какое-то точное значение в этом типе данных равно как самому длинному пути, так и половине максимального значения, которое может быть сохранено в этом типе данных, то это тривиальный выбор для BIG. В противном случае требуется более тщательный выбор, чтобы избежать округления или усечения.
если вы следили за всем этим, вы, вероятно, поймете один из лучших способов, которые я думал, было слишком сложно объяснить: это удвоит размер элемента, но вырезать элемент считай до половины. Он получит все преимущества настройки std:: map для базового дизайна без стоимости журнала (P). Это сократит средний путь времени вниз, не повредив время патологических случаев.
определите структуру CB, которая содержит стоимость и черный счетчик. Основным хранилищем является vector<vector<CB>>. Внешний вектор имеет одну позицию для каждой допустимой комбинации J,R. Они находятся в регулярном шаблоне, поэтому мы могли бы легко вычислить положение в векторе данного J, R или J, R данная позиция. Но быстрее сохранить их постепенно, поэтому J и R подразумеваются, а не используются напрямую. Вектор должен быть зарезервирован до его конечного размера, который составляет приблизительно N^2/4. Возможно, будет лучше, если вы предварительно вычислите индекс для H,0
каждый внутренний вектор имеет пары C,B в строго возрастающей последовательности b и внутри каждого S, строго уменьшая последовательность C. Внутренние векторы генерируются по одному за раз (во временном векторе) , а затем копируются в их окончательный местоположение и только чтение (не изменено) после этого. В рамках генерации каждого внутреннего вектора, кандидаты C, B пары будут генерироваться в возрастающей последовательности B. Поэтому держите позицию bestOdd и bestEven при построении вектора температуры. Затем каждый кандидат помещается в вектор только в том случае, если он имеет более низкий C, чем best (или best еще не существует). Мы также можем лечить всех B<P+J-N как будто B==S настолько ниже C в этом диапазоне заменяет, а не толкает.
подразумеваемые (никогда не сохраняемые) пары J,R внешнего вектора начать с (0,0) (1,0) (1,1) (2,0) и заканчивается на (N-1, H-1) (N-1,H) (N,H). Быстрее всего работать с этими индексами постепенно, поэтому, когда мы вычисляем вектор для подразумеваемой позиции J, R, у нас будет V как фактическое положение J, R и U как фактическое положение J-1, R и minU как первое положение J-1,? и minV как первая позиция J,? и minW как первая позиция J+1,?
Во внешнем цикле мы тривиально копируем minV в minU и minW и minV и V, и довольно легко вычислить новый minW и решить, начинается ли U с minU или minU+1.
цикл внутри, который продвигает V до (но не включая) minW, продвигая U каждый раз, когда V продвигается, и в типичных позициях, используя вектор в позиции U-1 и вектор в позиции U вместе, чтобы вычислить вектор для позиции V. Но вы должны охватить частный случай U==minU, в котором вы не используете вектор в U-1 и частный случай U==minV, в котором вы используете только вектор в U-1.
при объединении двух векторов вы проходите через них синхронно по значению B, используя один или другой для создания кандидата (см. выше), на основе которого вы сталкиваетесь со значениями B.
концепция: предполагая, что вы понимаете,как хранится значение с подразумеваемыми J,R и явным C, B: его значение заключается в том, что существует путь к столбцу J по стоимости C, используя ровно R красных ветвей и точно B черных ветвей и не существует существует путь к столбцу J, используя ровно R красных ветвей и тот же S, в котором один из C' или B' лучше и не хуже других.
кажется Динамическое Программирование проблема для меня.
In here, v,u are arbitrary nodes.
Source node: s
Target node: t
For a node v, such that its outgoing edges are (v,u1) [red/blue], (v,u2) [black].
D(v,i,k) = min { ((v,u1) is red ? D(u1,i+1,k) : D(u1,i-1,k)) + w(v,u1) ,
D(u2,i,k-1) + w(v,u2) }
D(t,0,k) = 0 k <= p
D(v,i,k) = infinity k > p //note, for any v
D(t,i,k) = infinity i != 0
объяснение:
- v-текущий узел
- i - #reds_traversed - #blues_traversed
- k - #black_edges_left
предложения stop находятся в целевом узле, вы заканчиваетесь при достижении его и разрешаете достигать его только с i=0 и с k
рекурсивный вызов проверяет в каждой точке "что лучше? идущий через черный или идя, хотя красный / синий", и выбирая лучшее решение из обоих вариантов.
идея состоит в том, D(v,i,k) - оптимальный результат для перехода от v к целевому (t),#reds-#blues используется i, а вы можете использовать k черные края.
из этого можно сделать вывод D(s,0,p) является оптимальным результатом для достижения цели из источника.
С |i| <= n, k<=p<=n - общее время работы алгоритма -O(n^3), предполагая, что реализовано в динамическом Программирование.
ваш экспоненциальный алгоритм по существу является деревом поиска глубины, где вы отслеживаете стоимость по мере спуска.
вы могли бы сделать его ветвь и привязку, отслеживая лучшее решение, виденное до сих пор, и обрезать любые ветви, которые будут выходить за рамки лучшего до сих пор.
или, вы можете сделать его широтно-первым поиском, заказанным по стоимости, так что, как только вы найдете какое-либо решение, оно будет одним из лучших.
Так, как я делал это в прошлом глубина-первая, но с бюджет. Я обрезаю все ветви, которые выходят за рамки бюджета. Затем я запускаю, если с бюджетом 0. Если он не находит никаких решений, я запускаю его с бюджетом 1. Я продолжаю увеличивать бюджет, пока не найду решение. Это может показаться большим повторением, но поскольку каждый запуск посещает намного больше узлов, чем предыдущий, предыдущие запуски не являются значительными.
Это экспоненциально в стоимости решения, а не в размере сети.