Поиск первого элемента списка Mathematica, превышающего порог

Джо правильно заявляет в своем ответ что можно было бы ожидать, что метод бинарного поиска будет быстрее, чем Select, которые, похоже, просто выполняют линейный поиск, даже если список отсортирован:

ClearAll[selectTiming]
selectTiming[length_, iterations_] := Module[
    {lst},
    lst = Sort[RandomInteger[{0, 100}, length]];
    (Do[Select[lst, # == 2 &, 1], {i, 1, iterations}] // Timing // 
     First)/iterations
  ]

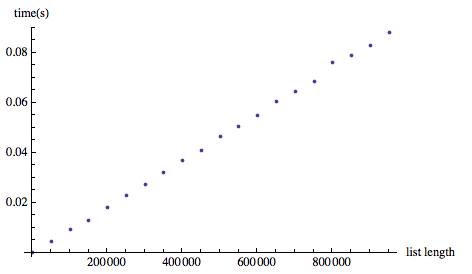
(я произвольно поставил порог в 2 для демонстрационных целей).

чтобы получить самый левый элемент, который больше порога, учитывая упорядоченный список, мы можем продолжить либо рекурсивно:

binSearch[lst_,threshold_]:= binSearchRec[lst,threshold,1,Length@lst]

(*
return position of leftmost element greater than threshold
breaks if the first element is greater than threshold
lst must be sorted
*)
binSearchRec[lst_,threshold_,min_,max_] :=
    Module[{i=Floor[(min+max)/2],element},
        element=lst[[i]];
        Which[
            min==max,max,
            element <= threshold,binSearchRec[lst,threshold,i+1,max],
            (element > threshold) && ( lst[[i-1]] <= threshold ), i,
            True, binSearchRec[lst,threshold,min,i-1]
        ]
    ]

или итерационно:

binSearchIterative[lst_,threshold_]:=Module[
    {min=1,max=Length@lst,i,element},
    While[
        min<=max,
        i=Floor[(min+max)/2];
        element=lst[[i]];
        Which[
            min==max, Break[],
            element<=threshold, min=i+1,
            (element>threshold) && (lst[[i-1]] <= threshold), Break[],
            True, max=i-1
        ]
    ];
    i
]

рекурсивный подход яснее, но я буду придерживаться итеративного.

чтобы проверить свою скорость,

ClearAll[binSearchTiming]
binSearchTiming[length_, iterations_] := Module[
    {lst},
    lst = Sort[RandomInteger[{0, 100}, length]];
    (Do[binSearchIterative[lst, 2], {i, 1, iterations}] // Timing // 
     First)/iterations
  ]

которая производит

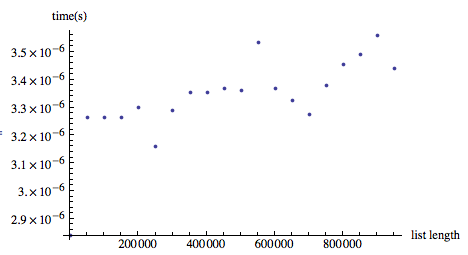
так, гораздо быстрее и лучше масштабирование поведения.

на самом деле нет необходимости компилировать его, но я все равно сделал.

в заключение, тогда не используйте Select для длинных списков.

на этом завершается мой ответ. Там следуют некоторые комментарии о выполнении двоичного поиска вручную или через пакет Combinatorica.

я сравнил скорость (скомпилированной) короткой процедуры, чтобы сделать двоичный поиск против BinarySearch С Combinatorica. Обратите внимание, что это не делает то, что задает вопрос (и ни делает BinarySearch С Combinatorica); код, который я дал выше.

двоичный поиск может быть реализован итерационно как

binarySearch = Compile[{{arg, _Integer}, {list, _Integer, 1}},
           Module[ {min = 1, max = Length@list,
                 i, x},
               While[
                    min <= max,
                    i = Floor[(min + max)/2];
                    x = list[[i]];
                    Which[
                         x == arg, min = max = i; Break[],
                         x < arg, min = i + 1,
                         True, max = i - 1
                     ]
                ];
               If[ 0 == max,
                   0,
                   max
               ]
           ], 
        CompilationTarget -> "C", 
        RuntimeOptions -> "Speed"
];

и теперь мы можем сравнить этот и BinarySearch С Combinatorica. Обратите внимание, что a) список должен быть отсортирован b) это не вернет первый соответствующий элемент, но a согласующего элемента.

lst = Sort[RandomInteger[{0, 100}, 1000000]];

давайте сравним две двоичные процедуры поиска. Повторяя 50000 раз:

Needs["Combinatorica`"]
Do[binarySearch[2, lst], {i, 50000}] // Timing
Do[BinarySearch[lst, 2], {i, 50000}] // Timing
(*
{0.073437, Null}
{4.8354, Null}
*)

так рукописный быстрее. Теперь, поскольку на самом деле двоичный поиск просто посещает 6-7 точек в списке для этих параметров (что-то вроде {500000, 250000, 125000, 62500, 31250, 15625, 23437} например), очевидно, что разница просто накладные расходы; возможно BinarySearch является более общим, например, или не компилируется.

вы можете посмотреть на TakeWhile[] и LengthWhile [], а также.

http://reference.wolfram.com/mathematica/ref/TakeWhile.html http://reference.wolfram.com/mathematica/ref/LengthWhile.html

list /. {___, y_ /; y > 3, ___} :> {y}

{3, 5, 4, 1} /. {___, y_ /; y > 3, ___} :> {y}

{5}

используя Select решает проблему, но это плохое решение, если вы заботитесь об эффективности. Select проходит по всем элементам списка и, следовательно, займет время, которое является линейным по длине списка.

Поскольку вы говорите, что список упорядочен, гораздо лучше использовать BinarySearch, который будет работать во времени, которое является логарифмическим по размеру списка. Выражение (редактировать: я сделал небольшую корректировку с предыдущего выражение, которое я написал, не обрабатывало правильно повторяющиеся элементы в списке. другое редактировать: это все еще не работает, когда сам порог появляется в списке как повторяющийся элемент, см. комментарии):

Floor[BinarySearch[list,threshold]+1]

даст вам индекс нужного элемента. Если все элементы меньше порога, вы получите длину списка плюс один.
С. С. не забудьте позвонить Needs["Combinatorica'"] перед использованием BinarySearch.

только для дальнейшего использования, начиная с v10 можно использовать SelectFirst

он имеет некоторые дополнительные тонкости, такие как возврат Missing[] или значения по умолчанию.

документы:

SelectFirst[{e1,e2,…}, crit] первый ei для чего crit[ei] is True или Missing["NotFound"] если ничего не найдено.

SelectFirst[{e1,e2,…}, crit, default] дает default если нет ei такое, что crit[ei] is True.

для вашего конкретного случая, вы можете использовать:

SelectFirst[list, # > threshold &]