Полиномиальный fit matlab с некоторыми ограничениями на коэффициенты

у меня есть данные, которые я должен интерполировать с помощью функции, которая должна быть следующего вида:

f(x) = ax4 + bx2 + c

С a > 0 и b ≤ 0. К сожалению, MATLAB polyfit не допускает каких-либо ограничений на коэффициенты полинома. Кто-нибудь знает, есть ли функция MATLAB для этого? В противном случае, как я могу его реализовать?

спасибо заранее,

Элизабетта

6
curve-fitting matlab

3 ответов

вы можете попробовать использовать fminsearch, fminunc определение целевой функции вручную.

кроме того, вы можете определить вашу проблему немного иначе:

f(x) = a2x4 - b2x2 + c

новая a и b можно оптимизировать для без ограничения, гарантируя, что окончательный a и b вы ищете положительные (отрицательные респ.).

11

без ограничений задача может быть записана и решена как простая линейная система:

% Your design matrix ([4 2 0] are the powers of the polynomial)
A = bsxfun(@power, your_X_data(:), [4 2 0]);

% Best estimate for the coefficients, [a b c], found by 
% solving A*[a b c]' = y in a least-squares sense
abc = A\your_Y_data(:)

эти ограничения, конечно, будут автоматически удовлетворены iff эта ограниченная модель действительно лежит в основе ваших данных. Например, 

% some example factors
a = +23.9;
b = -15.75;
c = 4;

% Your model
f = @(x, F) F(1)*x.^4 + F(2)*x.^2 + F(3);

% generate some noisy XY data
x = -1:0.01:1;
y = f(x, [a b c]) + randn(size(x));

% Best unconstrained estimate a, b and c from the data
A = bsxfun(@power, x(:), [4 2 0]);
abc = A\y(:);

% Plot results
plot(x,y, 'b'), hold on
plot(x, f(x, abc), 'r')
xlabel('x (nodes)'), ylabel('y (data)')

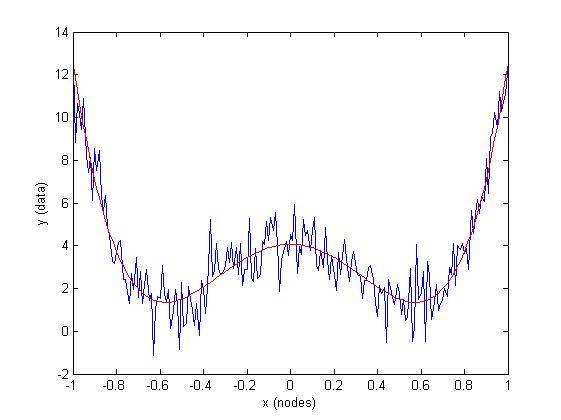
enter image description here

однако, если вы накладываете ограничения на данные, которые не точно описано этой ограниченной моделью, все может пойти неверно:

% Note: same data, but flipped signs 
a = -23.9;
b = +15.75;
c = 4;

f = @(x, F) F(1)*x.^4 + F(2)*x.^2 + F(3);

% generate some noisy XY data
x = -1:0.01:1;
y = f(x, [a b c]) + randn(size(x));

% Estimate a, b and c from the data, Forcing a>0 and b<0
abc = fmincon(@(Y) sum((f(x,Y)-y).^2), [0 0 0], [-1 0 0; 0 +1 0; 0 0 0], zeros(3,1));

% Plot results
plot(x,y, 'b'), hold on
plot(x, f(x, abc), 'r')
xlabel('x (nodes)'), ylabel('y (data)')

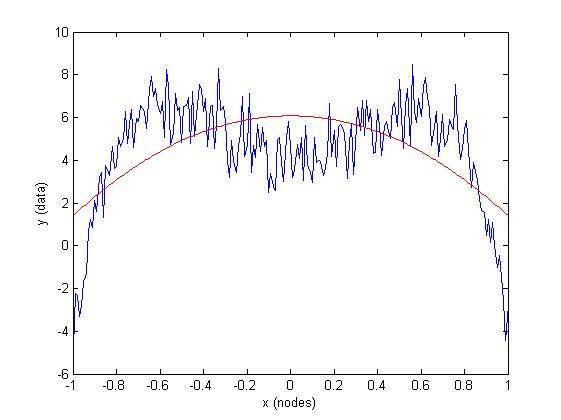
enter image description here

(решение a == 0, что указывает на неправильный выбор модели).

если точное равенство a == 0 проблема: конечно, нет никакой разницы, если вы установите a == eps(0). Численно это не будет заметно для реальных данных, но тем не менее это ненулевое значение.

во всяком случае, у меня есть подозрение, что ваша модель выбрана не очень хорошо, и ограничения-это "исправление", чтобы заставить все работать или ваши данные на самом деле должен быть беспристрастным/масштабированным, прежде чем пытаться сделать какую-либо подгонку или что применяются некоторые аналогичные предварительные условия (я часто видел, как люди делают такие вещи, поэтому да, я немного предвзят в этом отношении :).

так...каковы реальные причины этих трудностей?

7

Если у вас есть набор инструментов для подгонки кривой, то fit позволяет устанавливать ограничения с помощью параметров "верхний" и "Нижний". Вы бы хотели что-то подобное.

M=fit(x, f, 'poly4', 'upper', [-inf, 0, -inf, 0, -inf], 'lower', [0, 0, 0, 0, -inf]);

Примечание используйте-inf, чтобы установить определенный коэффициент, который должен быть неограниченным.

Это даст объект cfit с соответствующими коэффициентами. Вы можете получить к ним доступ, используя, например, M. p1 для термина x^4. В качестве альтернативы вы можете оценить функцию в любых точках, которые вы хотите использовать feval.

Я думаю,вы можете сделать аналогичную вещь, используя lsqcurvefit в панели инструментов оптимизации.

3