Построение системы компьютерной алгебры
Я создаю CAS (систему компьютерной алгебры) в PHP, но я застрял прямо сейчас. Я использую этот сайт.
теперь я написал токенизатор. Он преобразует уравнение следующим образом:
1+2x-3*(4-5*(3x))
для этого:
NUMBER PLUS_OPERATOR NUMBER VAR[X] MINUS_OPERATOR NUMBER MULTIPLY_OPERATOR GROUP
(где group-другой набор токенов). Как я могу упростить это уравнение? Да, я знаю, что вы можете сделать: добавить X-vars, но они находятся в подгруппе. Какой лучший метод я могу использовать для обработки этих токенов?
3 ответов
действительно полезным следующим шагом было бы построить дерево разбора:
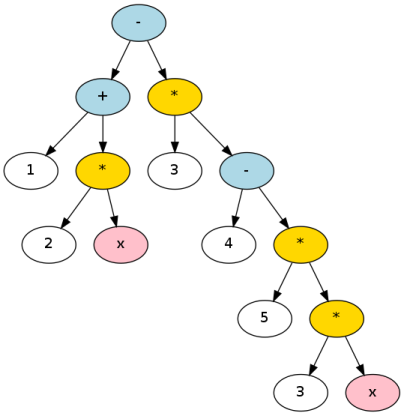
вы бы сделали один из них, написав синтаксический анализатор. Вы можете сделать это, написав простой рекурсивный парсер спуска или введя большие пушки и использование генератора синтаксического анализатора. В любом случае, это помогает построить формальную грамматику:
expression: additive
additive: multiplicative ([+-] multiplicative)*
multiplicative: primary ('*' primary)*
primary: variable
| number
| '(' expression ')'
заметим, что эта грамматика не обрабатывает 2x синтаксис, но это должно быть легко добавлять.
обратите внимание на умное использование рекурсии в правилах грамматики. primary захватывает только переменные, числа и выражения в скобках и останавливается, когда он сталкивается с оператором. multiplicative анализирует один или несколько primary выражениями-символами * знаки, но останавливается, когда он работает в + или - знак. additive анализирует один или несколько multiplicative выражениями-символами + и -, но останавливается, когда он работает в ). Следовательно, схема рекурсии определяет приоритет оператора.
это не слишком сложно реализовать предиктивный синтаксический анализатор вручную, как я сделал ниже (см. полный пример на ideone.com):
function parse()
{
global $tokens;
reset($tokens);
$ret = parseExpression();
if (current($tokens) !== FALSE)
die("Stray token at end of expression\n");
return $ret;
}
function popToken()
{
global $tokens;
$ret = current($tokens);
if ($ret !== FALSE)
next($tokens);
return $ret;
}
function parseExpression()
{
return parseAdditive();
}
function parseAdditive()
{
global $tokens;
$expr = parseMultiplicative();
for (;;) {
$next = current($tokens);
if ($next !== FALSE && $next->type == "operator" &&
($next->op == "+" || $next->op == "-"))
{
next($tokens);
$left = $expr;
$right = parseMultiplicative();
$expr = mkOperatorExpr($next->op, $left, $right);
} else {
return $expr;
}
}
}
function parseMultiplicative()
{
global $tokens;
$expr = parsePrimary();
for (;;) {
$next = current($tokens);
if ($next !== FALSE && $next->type == "operator" &&
$next->op == "*")
{
next($tokens);
$left = $expr;
$right = parsePrimary();
$expr = mkOperatorExpr($next->op, $left, $right);
} else {
return $expr;
}
}
}
function parsePrimary()
{
$tok = popToken();
if ($tok === FALSE)
die("Unexpected end of token list\n");
if ($tok->type == "variable")
return mkVariableExpr($tok->name);
if ($tok->type == "number")
return mkNumberExpr($tok->value);
if ($tok->type == "operator" && $tok->op == "(") {
$ret = parseExpression();
$tok = popToken();
if ($tok->type == "operator" && $tok->op == ")")
return $ret;
else
die("Missing end parenthesis\n");
}
die("Unexpected $tok->type token\n");
}
хорошо, теперь у вас есть это прекрасное дерево разбора, и даже красивая картина, чтобы пойти с ним. И что теперь? Ваша цель (на данный момент) может быть просто объединить условия, вы получите результат в виде:
n1*a + n2*b + n3*c + n4*d + ...
эту часть я оставляю вам. Имея разбор дерево должно сделать все намного проще.
PHP хорош в строках, числах и массивах. Но это плохой язык для реализации манипуляции символическими формулами, потому что у него нет собственного механизма обработки "символических выражений", для которых вы действительно хотите деревья. Да, вы можете реализовать весь этот механизм. Что труднее выполнить алгебраические манипуляции. Его довольно много работы, если вы хотите построить что-то полу-сложные. В идеале вы хотите, чтобы машины помогли вам написать преобразования прямо и легко.
например, как вы будете реализовывать произвольные правила алгебры? Ассоциативность и коммутативность? Термин "соответствие на расстоянии"? например,
(3*a+b)-2(a-b)+a ==> 3a-b
вы можете посмотреть как простой CAS может быть реализован используя наш система преобразования программы DMS. DMS имеет жесткие математические конструкции, такие как коммутативность и ассоциативность, и вы можете писать правила алгебры явно для работы с символическими формулами.
книга компьютерная Алгебра и символьные вычисления: математические методы Джоэла С. Коэна описывается алгоритм автоматического упрощения алгебраических выражений.
этот алгоритм используется в символизм библиотека компьютерной алгебры для C#. Следуя вашему примеру, следующая программа на C#:
var x = new Symbol("x");
(1 + 2 * x - 3 * (4 - 5 * (3 * x)))
.AlgebraicExpand()
.Disp();
отображает на консоли следующее:
-11 + 47 * x
