Повторите копии элементов массива: декодирование длины выполнения в MATLAB
Я пытаюсь вставить несколько значений в массив, используя массив "значения" и массив "счетчик". Например, если:
a=[1,3,2,5]
b=[2,2,1,3]
Я хочу вывод некоторой функции
c=somefunction(a,b)
на
c=[1,1,3,3,2,5,5,5]
где a(1) повторяется b(1) количество раз, a(2) повторяется b (2) раз и т. д...
есть ли встроенная функция в MATLAB, которая делает это? Я бы хотел избежать использования цикла for, если это возможно. Я пробовал варианты "repmat ()" и " kron ()", чтобы нет выгода.
это в принципе Run-length encoding.
5 ответов
Постановка Задачи
у нас есть массив значений, vals и runlengths, runlens:
vals = [1,3,2,5]
runlens = [2,2,1,3]
мы должны повторить каждый элемент в vals раз каждый соответствующий элемент runlens. Таким образом, конечный результат будет:
output = [1,1,3,3,2,5,5,5]
Перспективный Подход
одним из самых быстрых инструментов с MATLAB является cumsum и очень полезно при решении проблем векторизации, которые работают на нерегулярных шаблонах. В заявленная проблема, нерегулярность приходит с различными элементами в runlens.
теперь, чтобы использовать cumsum, нам нужно сделать две вещи: инициализировать массив zeros и поместите "соответствующие" значения в" ключевые "позиции над массивом нулей, так что после"cumsum" применяется, мы бы в конечном итоге с окончательным массивом повторяется vals of runlens раза.
действия: давайте пронумеруем вышеупомянутые шаги, чтобы дать перспективный подход более легкая перспектива:
1) инициализировать массив нулей: какова должна быть длина? Так как мы повторяем runlens раз, длина массива нулей должна быть суммированием всех runlens.
2) найти ключевые позиции / индексы: теперь эти ключевые позиции являются местами вдоль массива нулей, где каждый элемент из vals начать повторять.
Таким образом, для runlens = [2,2,1,3], ключевые позиции, отображаемые на массив нулей, будут:
[X 0 X 0 X X 0 0] % where X's are those key positions.
3) Найдите соответствующие значения: окончательный гвоздь должен быть забит перед использованием cumsum было бы поставить "соответствующие" значения в эти ключевые позиции. Теперь, так как мы будем делать cumsum вскоре после этого, если вы внимательно подумайте, вам понадобится differentiated версия values С diff, так что cumsum на них вернуть values. Поскольку эти дифференцированные значения будут помещены в массив нулей в местах, разделенных runlens расстояния, после использования cumsum мы бы друг vals элемент повторяется runlens времена как окончательный выход.
Код Решения
вот реализация, сшивающая все вышеупомянутые шаги -
% Calculate cumsumed values of runLengths.
% We would need this to initialize zeros array and find key positions later on.
clens = cumsum(runlens)
% Initalize zeros array
array = zeros(1,(clens(end)))
% Find key positions/indices
key_pos = [1 clens(1:end-1)+1]
% Find appropriate values
app_vals = diff([0 vals])
% Map app_values at key_pos on array
array(pos) = app_vals
% cumsum array for final output
output = cumsum(array)
предварительное распределение Hack
как видно, в приведенном выше коде используется предварительное выделение с нулями. Теперь, согласно этому недокументированный блог MATLAB на более быстром предварительном выделении, можно достичь гораздо быстрее предварительное выделение с -
array(clens(end)) = 0; % instead of array = zeros(1,(clens(end)))
завершение: код функции
чтобы обернуть все, у нас был бы компактный код функции для достижения этого декодирования длины пробега, как так -
function out = rle_cumsum_diff(vals,runlens)
clens = cumsum(runlens);
idx(clens(end))=0;
idx([1 clens(1:end-1)+1]) = diff([0 vals]);
out = cumsum(idx);
return;
бенчмаркинг
Бенчмаркинг Код
указан следующий код сравнивает runtimes и ускорений для указанных cumsum+diff подходите в этом посте над другое cumsum-only на основе подходи!--59-- > on MATLAB 2014B-
datasizes = [reshape(linspace(10,70,4).'*10.^(0:4),1,[]) 10^6 2*10^6]; %
fcns = {'rld_cumsum','rld_cumsum_diff'}; % approaches to be benchmarked
for k1 = 1:numel(datasizes)
n = datasizes(k1); % Create random inputs
vals = randi(200,1,n);
runs = [5000 randi(200,1,n-1)]; % 5000 acts as an aberration
for k2 = 1:numel(fcns) % Time approaches
tsec(k2,k1) = timeit(@() feval(fcns{k2}, vals,runs), 1);
end
end
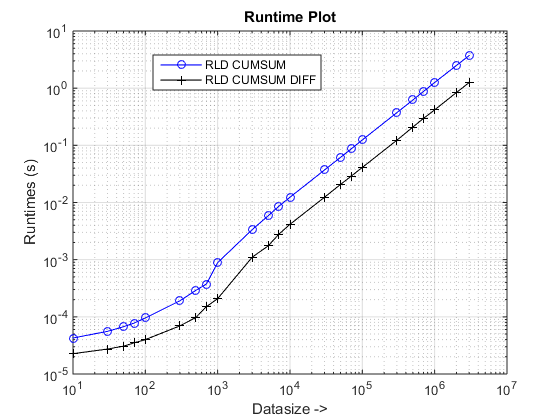
figure, % Plot runtimes
loglog(datasizes,tsec(1,:),'-bo'), hold on
loglog(datasizes,tsec(2,:),'-k+')
set(gca,'xgrid','on'),set(gca,'ygrid','on'),
xlabel('Datasize ->'), ylabel('Runtimes (s)')
legend(upper(strrep(fcns,'_',' '))),title('Runtime Plot')
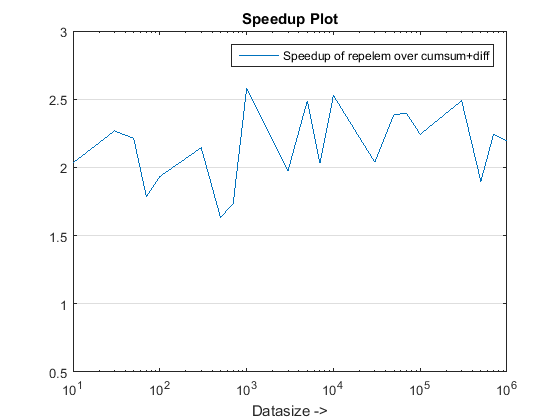
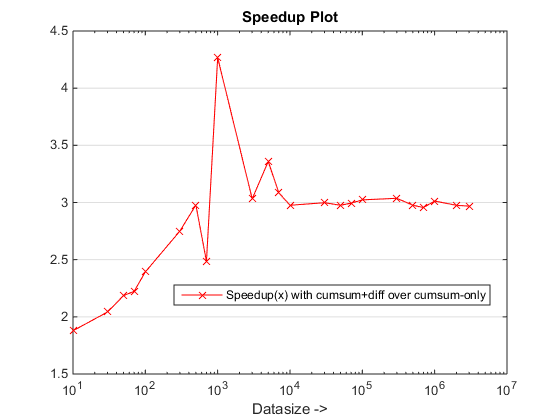
figure, % Plot speedups
semilogx(datasizes,tsec(1,:)./tsec(2,:),'-rx')
set(gca,'ygrid','on'), xlabel('Datasize ->')
legend('Speedup(x) with cumsum+diff over cumsum-only'),title('Speedup Plot')
связанный код функции для rld_cumsum.m:
function out = rld_cumsum(vals,runlens)
index = zeros(1,sum(runlens));
index([1 cumsum(runlens(1:end-1))+1]) = 1;
out = vals(cumsum(index));
return;
графики выполнения и ускорения
выводы
предлагаемый подход, похоже, дает нам заметное ускорение по сравнению с cumsum-only подход, который о 3x!
почему это новое cumsum+diff подход лучше, чем предыдущий cumsum-only подход?
Ну, суть причины лежит на заключительном этапе cumsum-only подход, который должен отображать значения "cumsumed" в vals. В новом cumsum+diff подход, мы делаем diff(vals) вместо этого MATLAB обрабатывает только n элементов (где n-количество runLengths) по сравнению с отображение sum(runLengths) количество элементов cumsum-only подход, и это число должны быть во много раз больше, чем n и поэтому заметное ускорение с этим новым подходом!
критерии
обновлено для R2015b: repelem сейчас самый быстрый для всех размеров данных.
проверено функций:
- встроенный MATLAB
repelemфункция, которая была добавлена в R2015a - gnovice это
cumsumрешение (rld_cumsum) - Divakar это
cumsum+diffрешение (rld_cumsum_diff) - knedlsepp это
accumarrayрешение (knedlsepp5cumsumaccumarray) от этот пост - наивная реализация на основе цикла (
naive_jit_test.m) для проверки компилятора just-in-time
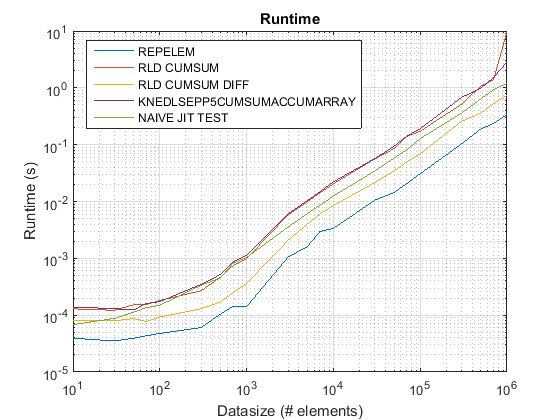
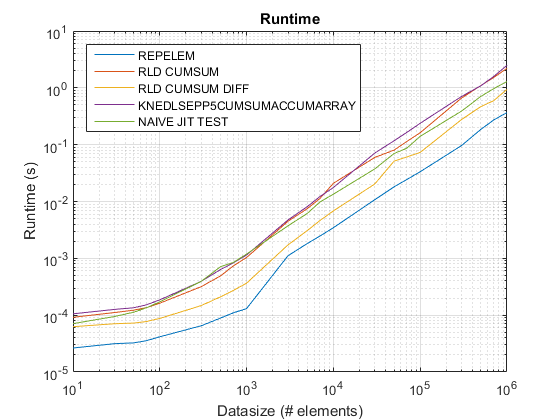
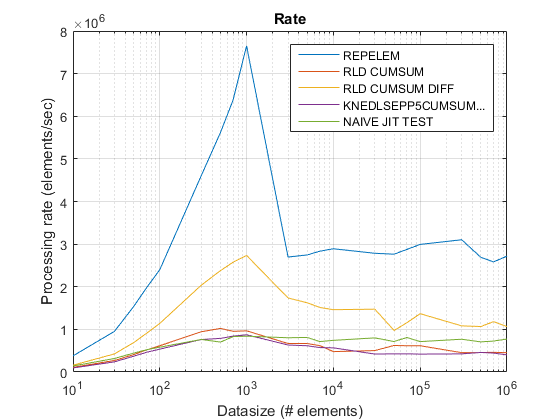
результаты test_rld.m на R2015b:
старый график времени с использованием R2015a здесь.
выводы:
-
repelemis всегда быстрее примерно в 2 раза. -
rld_cumsum_diffпоследовательно быстрее, чемrld_cumsum. repelemявляется самым быстрым для небольших размеров данных (менее 300-500 элементов)rld_cumsum_diffстановится значительно быстрее, чемrepelemоколо 5 000 элементовrepelemбудет медленнее, чемrld_cumsumгде-то между 30 000 и 300 000 элементов-
rld_cumsumимеет примерно такую такая же производительность, какknedlsepp5cumsumaccumarray -
naive_jit_test.mимеет почти постоянную скорость и наравне сrld_cumsumиknedlsepp5cumsumaccumarrayдля меньших размеров, немного быстрее для больших размеров
старому курсу сюжет, используя R2015a здесь.
вывод
использовать repelem ниже около 5 000 элементов и .cumsum+diff решение выше
Я не знаю встроенной функции, но вот одно решение:
index = zeros(1,sum(b));
index([1 cumsum(b(1:end-1))+1]) = 1;
c = a(cumsum(index));
объяснение:
вектор нулей сначала создается той же длины, что и выходной массив (т. е. сумма всех репликаций в b). Затем они помещаются в первый элемент и каждый последующий элемент, представляющий, где начало новой последовательности значений будет в выходных данных. Совокупная сумма вектора index затем можно использовать для индексирования в a, репликация каждого значения нужное количество раз.
для ясности, это то, что различные векторы выглядят как для значений a и b дали в вопросе:
index = [1 0 1 0 1 1 0 0]
cumsum(index) = [1 1 2 2 3 4 4 4]
c = [1 1 3 3 2 5 5 5]
EDIT: для полноты картины, есть и другая альтернатива с помощью ARRAYFUN, но это, кажется, занимает от 20-100 раз больше времени, чем вышеупомянутое решение с векторами до 10 000 элементов долго:
c = arrayfun(@(x,y) x.*ones(1,y),a,b,'UniformOutput',false);
c = [c{:}];
есть наконец (по состоянию на R2015a) встроенная и документированная функция для этого,repelem. Здесь уместен следующий синтаксис, где второй аргумент является вектором:
W = repelem(V,N), с векторомVи VectorN, создает векторWгде элементV(i)повторяетсяN(i)раза.
или, другими словами, " каждый элемент N указывает количество повторов соответствующий элемент V."
пример:
>> a=[1,3,2,5]
a =
1 3 2 5
>> b=[2,2,1,3]
b =
2 2 1 3
>> repelem(a,b)
ans =
1 1 3 3 2 5 5 5
проблемы производительности во встроенном MATLAB repelem было исправлено в R2015b. Я запустил test_rld.m программа из сообщения chappjc в R2015b и repelem теперь быстрее, чем другие алгоритмы примерно в 2: