Преобразование неориентированного графа в дерево
предоставлена неориентированный граф в котором каждый узел имеет декартову координату в пространстве, которая имеет общую форму дерева, есть ли алгоритм преобразования графика в дерево и найти соответствующий корневой узел?
обратите внимание, что наше определение "дерева" требует, чтобы ветви не расходились от родительских узлов под острыми углами.
см. примеры графиков ниже. Как мы найдем Красный Узел?
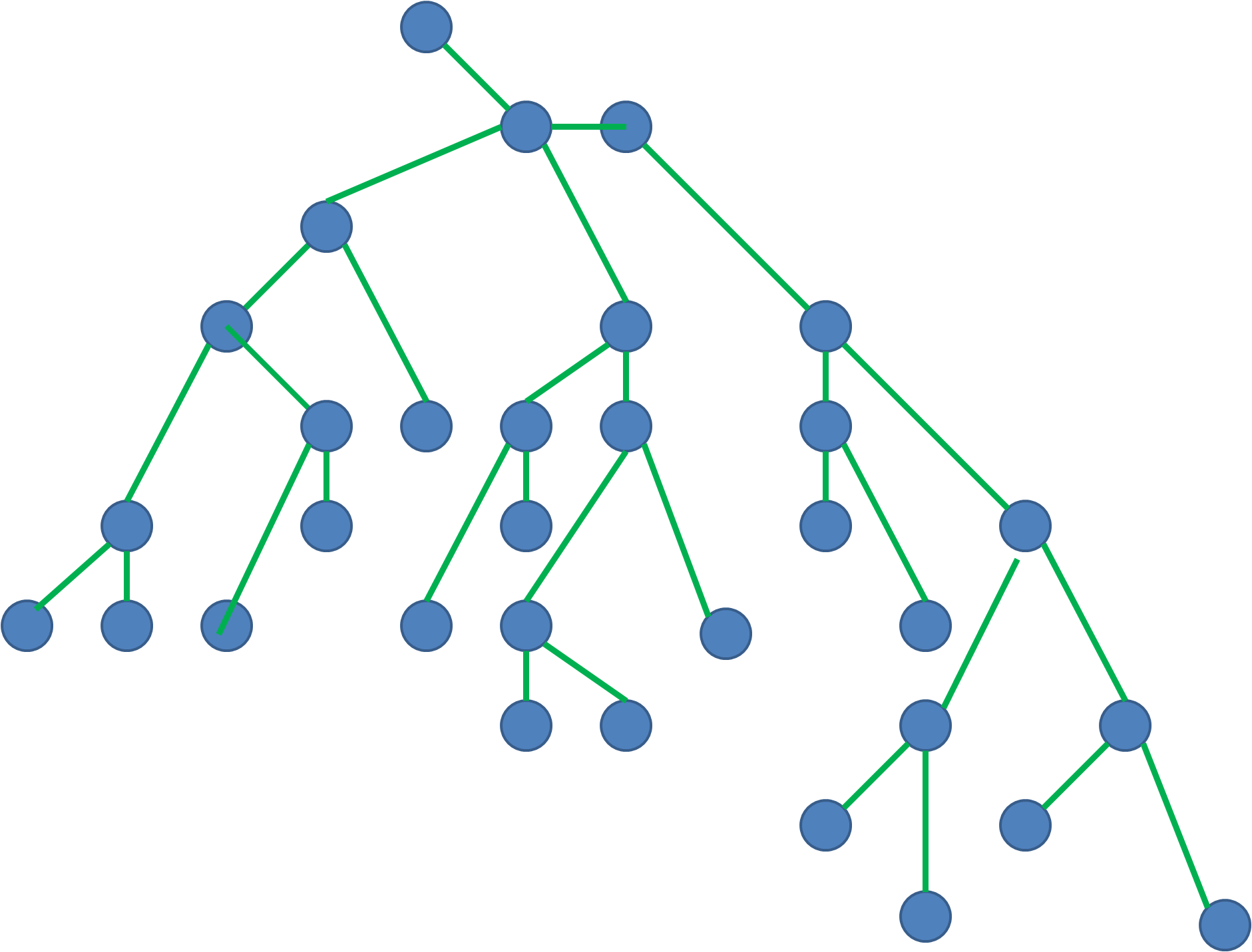
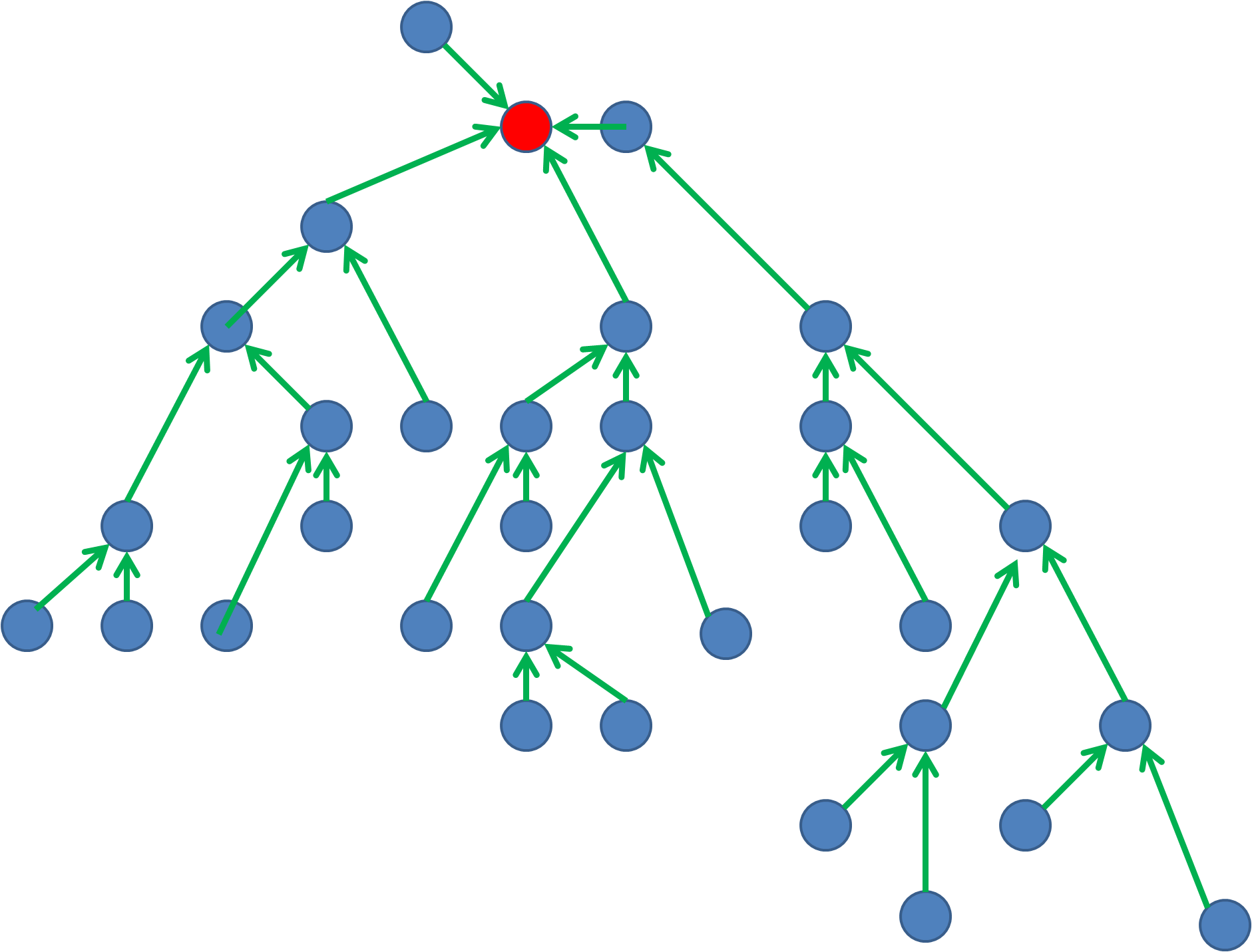
2 ответов
здесь предложение о том, как решить вашу проблему.
предпосылки
- Примечание:
-
gграфикаg.vвершин графа -
v,w,z: отдельные вершины -
e: индивидуальные краю -
n: количество вершин
-
- любая комбинация неориентированного дерева g и заданного узла g.V однозначно определяет направленное дерево с корнем g.v (доказуемо индукцией)
идея
- дополнить края
gпо ориентациям в направленном дереве, подразумеваемымgи еще не найденный корневой узел локальными вычислениями в узлахg. - эти ориентации будут представлять дочерние-родительские-relationsships между узлами (
v -> w:vребенка,wparent). - полностью отмеченное дерево будет содержать единственный узел с outdegree 0, который является желаемый корневой узел. вы можете получить 0 или более одного корневого узла.
алгоритм
предполагает стандартное представление структуры графика / дерева (например, список смежности)
- все вершины в
g.vизначально помечены как не посещенные, не законченные. -
посетить все вершины в произвольном порядке. пропустить узлы, помеченные как "готово".
пустьvбыть посещаемой вершиной.- 2.1 развертки через все края, связывающие
vпо часовой стрелке, начиная со случайно выбранногоe_0в порядке угла ребер сe_0. -
2.2. ориентация смежных ребер
e_1=(v,w_1), e_2(v,w_2), которые охватывают острый угол.
смежный: wrt упорядочивается в соответствии с углом, который они заключают вe_0.[ Примечание: существование такой пары не гарантируется, см. 2-й комментарий и последнее замечание. если нет острого угла, перейти на 2. со следующим узлом. ]
-
2.2.1 положения края
e_1, e_2известны:-
w_1 -> v -> w_2: невозможно, так как дедушка-ребенок-сегмент будет заключать острый угол -
w_1 <- v <- w_2: невозможно, по той же причине w_1 <- v -> w_2: невозможно, нет узлов с outdegree >1 в деревеw_1 -> v <- w_2:
возможна только пара ориентаций.e_1, e_2может были ориентированы раньше. если предыдущая ориентация нарушает текущее назначение, экземпляр проблемы не имеет решения.
-
-
2.2.2 это назначение подразумевает древовидную структуру на подграфах, индуцированных всеми вершинами, достижимыми из
w_1(w_2) на пути, не включающемe_1 (e_2`). отметьте все вершины в обоих индуцированных поддеревьях как законченные[ Примечание: структура поддерева может нарушать ограничения угла. в в этом случае проблема не имеет решения. ]
-
-
2.3 метки
vпосетил. после завершения шагов 2.2 в vertexvпроверьте количествоncсоединяющихся ребер, которым еще не назначена ориентация.-
nc = 0: это корень, который вы искали , но вы должны проверить, совместимо ли решение с вашими ограничениями. -
nc = 1: пусть этот край будет(v,z).
ориентация этого ребра v - >z, как вы находитесь в дереве. Марк v как законченный.- 2.3.1 проверить
zпомечено ли оно готово. если это не так, проверьте номерnc2из неориентированных ребер, соединяющихz.nc2= 1: повторите шаг 2.3, взявzнаv.
- 2.3.1 проверить
-
- 2.1 развертки через все края, связывающие
если вы еще не нашли корневой узел, экземпляр проблемы неоднозначен: ориентируйте оставшиеся неориентированные края по желанию.
Примечания
-
прекращение: каждый узел посещается максимум 4 раза:
- один раз на Шаг 2
- на максимальном дважды в шаг 2.2.2
- на максимальном раз в шаг 2.3
-
правильность:
- все края заключая острый угол ориентированы в шаг 2.2.1
-
сложность (время):
- посещение каждого узла: O (n);
-
развертка по часовой стрелке через все ребра, соединяющие данную вершину, требует сортировки этих ребер.
таким образом, вам нужноO( sum_i=1..m ( k_i * lg k_i ) )atm <= nвершины под ограничениемsum_i=1..m k_i = n.в общей сложности это требует
O ( n * lg n), assum_i=1..m ( k_i * lg k_i ) <= n * lg nданоsum_i=1..m k_i = nлюбойm <= n(доказуемо путем применения оптимизации Лагранжа).[ Примечание: Если ваши деревья имеют степень, ограниченную константой, вы теоретически сортируете в постоянное время на каждом затронутом узле; общая сумма в этом случае:
O(n)] -
поддерево обозначение:
каждый узел на графике посещается не более 2 раз этой процедурой, если она реализована как dfs. таким образом, в общей сложностиO(n)для вызова этой подпрограммы.в итоге:
O(n * lg n)
-
сложности (пространство):
-
O(n)для сортировки (с вершинной степенью, не связанной с константой).
-
-
проблема, вероятно, плохо определена:
- несколько решений: например, steiner tree
- нет решения: например, график в форме стрелки с двойным наконечником ( )
простым решением было бы определить 2d-прямоугольник вокруг красного узла или центра вашего узла и вычислить каждый узел с кривой Мура. Кривая Мура-это кривая заполнения пространства, больше по специальной версии кривой Гильберта, где начальная и конечная вершины одинаковы, а координата находится в середине 2d-прямоугольника. В generell ваша проблема выглядит как дискретная проблема пространства адресации.
