Преобразование системы координат в матрицу в Mathematica
перед вопросом программирования, я считаю, что мне нужно дать немного фона того, что я делаю, чтобы облегчить понимание моей проблемы :
Я записываю движения глаз при отображении некоторых шаблонов субъектам. В ходе эксперимента я позже продемонстрирую некоторое симметричное преобразование этих паттернов.
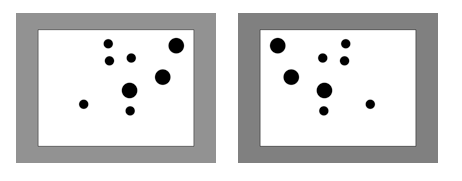
что я получаю, это списки координат фиксаций и длительности :
{{fix1X,fix1Y,fix1Dn},{fix2X,fix2Y,fix2Dn},...{fixNX, fixNY, fixNDn}}
где :
-fix1X - координата X для первой фиксации.
-fix1Y - координата Y для первой фиксации.
-fix1D - это длительность фиксаций в миллисекундах
Пожалуйста, обратите внимание :
FrameWidth = 31.36;
scrHeightCM = 30;
scrWidthCM = 40;
FrameXYs = {{4.32, 3.23}, {35.68, 26.75}}; (* {{Xmin,Ymin},{Xmax,Ymax}} *)
Ниже приведены фиксации для 1 дисплея (Фиксации субъекта во время презентации стимулов 3s на экране)
fix ={{20.14, 15.22, 774.}, {20.26, 15.37, 518.}, {25.65, 16.22, 200.},
{28.15, 11.06, 176.}, {25.25, 13.38, 154.}, {24.78, 15.74, 161.},
{24.23, 16.58, 121.}, {20.06, 13.22, 124.}, {24.91, 15.8, 273.},
{24.32, 12.83, 119.}, {20.06, 12.14, 366.}, {25.64, 18.22, 236.},
{24.37, 19.2, 177.}, {21.02, 16.4, 217.}, {20.63, 15.75,406.}}
Graphics[{
Gray, EdgeForm[Thick],
Rectangle @@ {{0, 0}, {scrWidthCM, scrHeightCM}},
White,
Rectangle @@ StimuliFrameCoordinates,
Dashed, Black,
Line[
{{(scrWidthCM/2), FrameXYs[[1, 2]]},
{(scrWidthCM/2), FrameXYs[[2, 2]]}}],
Line[
{{FrameXYs[[1, 1]], (scrHeightCM/2)},
{(FrameXYs[[2, 1]]), (scrHeightCM/2)}}],
Thickness[0.005], Pink,
Disk[{#[[1]], #[[2]]}, 9 N[#[[3]]/Total[fix[[All, 3]]]]] & /@ fix
}, ImageSize -> 500]
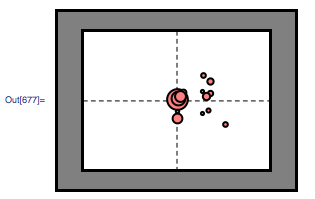
что я хочу сделать :
Я хотел бы "дискретизировать" пространство кадров стимулов в кластеры:
Ниже представлено визуальное представление (сделано в PPT) с различными кластерами (2,4,16,64).
цветная часть, представляющая кластеры, в которых произошли фиксации:
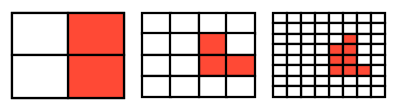
С это я хочу
-подсчитать количество записей в каждой группе.
- вычислите присутствие / количество или продолжительность, наблюдаемые в каждом кластере.
матричная форма легко позволит мне сравнить различные фиксации дисплеев путем вычитания.
Итак, вопрос(ы)
- как я могу создать гибкий механизм для разделения фрейма стимулов на кластеры.
-карта фиксации на тех кластеры, получающие прямоугольную матрицу, заполненную 0s или графами фиксаций или общей продолжительностью фиксаций для каждой ячейки матрицы.
Я чувствую, что этот вопрос может быть неясным и отредактирует его, чтобы прояснить все необходимое. Кроме того, как вы думаете, это должно быть задано в 2 отдельных вопросах, я рад это сделать.
большое спасибо заранее за любую помощь вы могли бы предоставить.
3 ответов
вы можете сделать что-то вроде:
createMatrix[list_, frameXYs_, partitX_, partitY_, fun_] :=
Module[{matrix},
(*init return matrix*)
matrix = Array[0 &, {partitX, partitY}];
(matrix[[
IntegerPart@Rescale[#[[1]], {frameXYs[[1, 1]], frameXYs[[2, 1]]}, {1,partitX}],
IntegerPart@Rescale[#[[2]], {frameXYs[[1, 2]], frameXYs[[2, 2]]}, {1,partitY}]
]] += fun[#[[3]]]) & /@ list;
Return@(matrix[[1 ;; -2, 1 ;; -2]]);]
здесь fun - это функция подсчета в третьем измерении вашего списка.
Итак, если вы хотите подсчитать вхождения:
fix = {{20.14, 15.22, 774.}, {20.26, 15.37, 518.}, {25.65, 16.22, 200.},
{28.15, 11.06, 176.}, {25.25, 13.38, 154.}, {24.78, 15.74, 161.},
{24.23, 16.58, 121.}, {20.06, 13.22, 124.}, {24.91, 15.8, 273.},
{24.32, 12.83, 119.}, {20.06, 12.14, 366.}, {25.64, 18.22, 236.},
{24.37, 19.2, 177.}, {21.02, 16.4, 217.}, {20.63, 15.75, 406.}};
FrameXYs = {{4.32, 3.23}, {35.68, 26.75}};
cm = createMatrix[fix, FrameXYs, 10, 10, 1 &]
MatrixPlot@cm
MatrixForm@cm
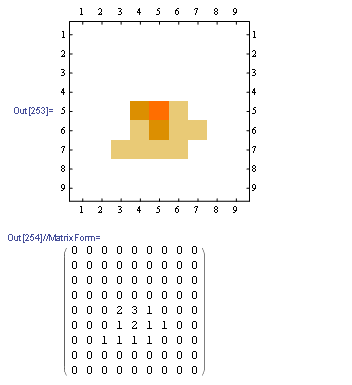
и если вы хотите добавить время фиксации
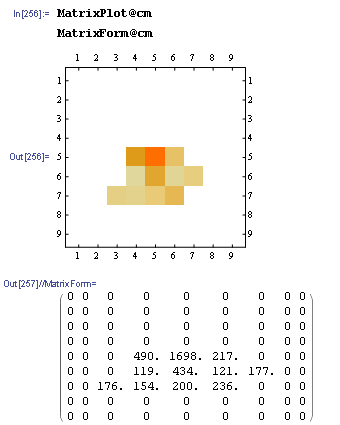
cm = createMatrix[fix, FrameXYs, 10, 10, # &]
MatrixPlot@cm
MatrixForm@cm
редактировать
внесение некоторых корректировок в индексы, небольшое приукрашивание кода, более четкое пример:
createMatrix[list_, frameXYs_, partit : {partitX_, partitY_}, fun_] :=
Module[{matrix, g},
(*Define rescale function*)
g[i_, l_] := IntegerPart@
Rescale[l[[i]], (Transpose@frameXYs)[[i]], {1, partit[[i]]}];
(*Init return matrix*)
matrix = Array[0 &, {partitX + 1, partitY + 1}];
(matrix[[g[1, #], g[2, #]]] += fun[#[[3]]]) & /@ list;
Return@(matrix[[1 ;; -2, 1 ;; -2]]);]
.
fix = {{1, 1, 1}, {1, 3, 2}, {3, 1, 3}, {3, 3, 4}, {2, 2, 10}};
FrameXYs = {{1, 1}, {3, 3}};
cm = createMatrix[fix, FrameXYs, {7, 7}, # &];
MatrixPlot@cm
Print[MatrixForm@SparseArray[(#[[1 ;; 2]] -> #[[3]]) & /@ fix], MatrixForm@cm]
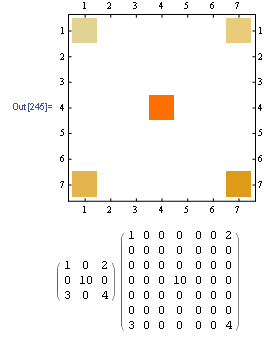
есть несколько вещей, которые необходимо сделать, чтобы выполнить то, что вы хотите. Во-первых, учитывая количество делений, мы должны разделить 2-мерное пространство. Во-вторых, используя счетчик делений, нам нужен гибкий метод группировки фиксаций в соответствующие места. Наконец, мы генерируем любую статистику, которая вам нужна.
что касается количества делений, встроенная функция FactorInteger почти делает то, что вам нужно. Для пример,
(* The second parameter is the upper limit for the number of factors returned *)
FactorInteger[35,2] == {{5,1}, {7,1}}
FactorInteger[64,2] == {{2,6}}
к сожалению, вы можете указать только верхний предел количества возвращаемых факторов, поэтому мы должны немного изменить вывод
Clear[divisionCount]
divisionCount[c_Integer?(Positive[#] && (# == 2 || ! PrimeQ[#]) &)] :=
With[{res = FactorInteger[c, 2]},
Power @@@ If[
Length[res] == 2,
res // Reverse,
With[
{q = Quotient[res[[1, 2]], 2], r = Mod[res[[1, 2]], 2],
b = res[[1, 1]]},
{{b, q + r}, {b, q}}
]
]
]
это делает две вещи, заменяет {{b,m}} С {{b, m / 2 + m mod 2}, {b, m / 2}} здесь / представляет целочисленное деление (т. е. остатки) и преобразует {{b, m} ..} to {b^m ..} via Power @@@. Это дает
divisionCount[32] == {8, 4}
divisionCount[64] == {8, 8}.
оказывается, мы можем получить количество фиксации в этот момент с минимальным дополнительная работа через BinCounts следующим образом
BinCounts[fix[[All,;;2]], (* stripping duration from tuples *)
{xmin, xmax, (xmax - xmin)/#1,
{ymin, ymax, (ymax - ymin)/#2]& @@ divisionCount[ divs ]
где вам нужно поставить ряды для x и y и количество дивизий. Однако это не так гибко, как могло бы быть. Вместо этого мы будем использовать SelectEquivalents.
ключ к использованию SelectEquivalents эффективно создает хорошую функцию категоризации. Для этого нам нужно самим определить деления, как следует
Clear[makeDivisions]
makeDivisions[
{xmin_, xmax_, xdivs_Integer?Positive}, {ymin_, ymax_, ydivs_Integer?Positive}] :=
Partition[#,2,1]& /@ {
(xmax - xmin)*Range[0, xdivs]/xdivs + xmin,
(ymax - ymin)*Range[0, ydivs]/ydivs + ymin
}
makeDivisions[
{xmin_, xmax_}, {ymin_, ymax_},
divs_Integer?(Positive[#] && (# == 2 || ! PrimeQ[#]) &)] :=
makeDivisions[{xmin, xmax, #1}, {ymin, ymax, #2}] & @@ divisionCount[divs]
здесь
makeDivisions[{0, 1}, {0, 1}, 6] ==
{{{0, 1/3}, {1/3, 2/3}, {2/3, 1}}, {{0, 1/2}, {1/2, 1}}}.
(я бы использовал FindDivisions, но он не всегда возвращает количество подразделений, которые вы запрашиваете.) makeDivisions возвращает два списка, где каждый член в каждом списке является парой min-max, которую мы можем использовать, чтобы определить, попадает ли точка в корзину.
поскольку мы находимся на квадратной решетке, нам нужно проверить все пары ограничений, которые мы только что определили. Я бы использовал следующее
Clear[inBinQ, categorize]
inBinQ[{xmin_,xmax_}, {ymin_, ymax_}, {x_,y_}]:=
(xmin <= x < xmax) && (ymin <= y < ymax)
categorize[{xmin_, xmax_}, {ymin_, ymax_}, divs_][val : {x_, y_, t_}] :=
With[{bins = makeDivisions[{xmin, xmax}, {ymin, ymax}, divs]},
Outer[inBinQ[#1, #2, {x, y}] &, bins[[1]], bins[[2]], 1]] //Transpose
что возвращает
categorize[{0,1},{0,1},6][{0.1, 0.2, 5}] ==
{{True, False, False}, {False, False, False}}.
обратите внимание, что координата y перевернута по сравнению с графиком, низкие значения находятся в начале массива. Чтобы "исправить" это, Reverse bins[[2]] на categorize. Кроме того, вы захотите удалить Transpose до предоставления результатов MatrixPlot, так как он ожидает результаты в untransposed форма.
используя
SelectEquivalents[
fix,
(categorize[{xmin, xmax}, {ymin, ymax}, 6][#] /. {True -> 1, False -> 0} &),
#[[3]] &, (* strip off all but the timing data *)
{#1, #2} &],
мы
{{
{{0, 0, 0}, {0, 1, 0}}, {774., 518., 161., 121., 273., 177., 217., 406.}
},
{
{{0, 0, 0}, {0, 0, 1}}, {200., 236.}
},
{
{{0, 0, 1}, {0, 0, 0}}, {176., 154.}
},
{
{{0, 1, 0}, {0, 0, 0}}, {124., 119., 366.}
}}}
где первый член в каждом подсписке является матричным представлением Бина и второй термин-это список точек, которые попадают в мусорку. Чтобы определить, сколько их в каждом бункере,
Plus @@ (Times @@@ ({#1, Length[#2]} & @@@ %)) ==
{{0, 3, 2}, {0, 8, 2}}
или, тайминги
Plus @@ (Times @@@ ({#1, Total[#2]} & @@@ %)) ==
{{0, 609., 330.}, {0, 2647., 436.}}
редактировать: как вы можете видеть, чтобы получить любую статистику, необходимую для фиксаций, вам просто нужно заменить либо Length или Total. Например, вы можете захотеть среднее значение (Mean) потраченное время, а не только общее.
В зависимости от вычислений, которые вы выполняете, и точности данных, вы можете позаботиться о более мягком подходе. Рассмотрите возможность использования для этого пересчета изображений. Вот один из возможных подходов. Здесь есть очевидная неясность, но опять же, это может быть желательно.
fix = {{20.14, 15.22, 774.}, {20.26, 15.37, 518.}, {25.65, 16.22,
200.}, {28.15, 11.06, 176.}, {25.25, 13.38, 154.}, {24.78, 15.74,
161.}, {24.23, 16.58, 121.}, {20.06, 13.22, 124.}, {24.91, 15.8,
273.}, {24.32, 12.83, 119.}, {20.06, 12.14, 366.}, {25.64, 18.22,
236.}, {24.37, 19.2, 177.}, {21.02, 16.4, 217.}, {20.63, 15.75,
406.}};
FrameXYs = {{4.32, 3.23}, {35.68, 26.75}};
Graphics[{AbsolutePointSize@Sqrt@#3, Point[{#, #2}]} & @@@ fix,
BaseStyle -> Opacity[0.3], PlotRange -> Transpose@FrameXYs,
PlotRangePadding -> None, ImageSize -> {400, 400}]
ImageResize[%, {16, 16}];
Show[ImageAdjust@%, ImageSize -> {400, 400}]

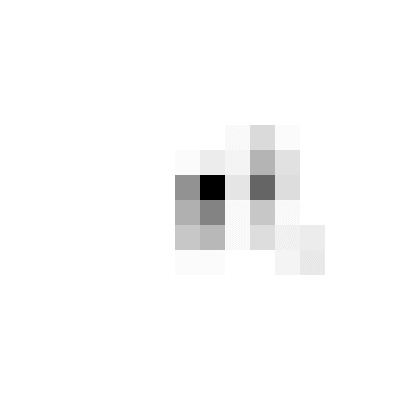
поскольку вышесказанное, по-видимому, бесполезно, вот попытка быть конструктивным. Это мой взгляд на прекрасное решение Велисария. Я чувствую, что это немного чище.
createMatrix[list_, {{x1_, y1_}, {x2_, y2_}}, par:{pX_, pY_}, fun_] :=
Module[{matrix, quant},
matrix = 0 ~ConstantArray~ par;
quant = IntegerPart@Rescale@## &;
(matrix[[
quant[#1, {x1, x2}, {1, pX}],
quant[#2, {y1, y2}, {1, pY}]
]] += fun[#3] &) @@@ list;
Drop[matrix, -1, -1]
]
обратите внимание, что синтаксис немного отличается: квантовать разделы x и y приведены в списке. Я чувствую, что это более согласуется с другими функциями, такими как Array.
