Производная от объяснения функции softmax
Я пытаюсь вычислить производную функции активации softmax. Я нашел это:https://math.stackexchange.com/questions/945871/derivative-of-softmax-loss-function никто, кажется, не дает правильного вывода для того, как мы получим ответы для i=j и i!= j. Кто-нибудь, пожалуйста, объясните это! Меня путают с производными, когда происходит суммирование, как в знаменателе для функции активации softmax.
2 ответов
производная суммы равна сумме производных, т. е.:
d(f1 + f2 + f3 + f4)/dx = df1/dx + df2/dx + df3/dx + df4/dx
для получения производных p_j С уважением o_i начнем:
d_i(p_j) = d_i(exp(o_j) / Sum_k(exp(o_k)))
я решил использовать d_i для производной по отношению к o_i сделать это легче читать.
Используя правило продукта мы получаем:
d_i(exp(o_j)) / Sum_k(exp(o_k)) + exp(o_j) * d_i(1/Sum_k(exp(o_k)))
глядя на первый член, производная будет 0 если i != j, это может быть представлено с Дельта функция который я буду называть D_ij. Это дает (для первого срока):
= D_ij * exp(o_j) / Sum_k(exp(o_k))
которая как раз наша первоначальная функция умноженная на D_ij
= D_ij * p_j
для второго члена, когда мы выводим каждый элемент суммы индивидуально, единственным ненулевым членом будет когда i = k, это дает нам (не забывая о правиле власти, потому что сумма находится в знаменателе)
= -exp(o_j) * Sum_k(d_i(exp(o_k)) / Sum_k(exp(o_k))^2
= -exp(o_j) * exp(o_i) / Sum_k(exp(o_k))^2
= -(exp(o_j) / Sum_k(exp(o_k))) * (exp(o_j) / Sum_k(exp(o_k)))
= -p_j * p_i
соединяя два вместе, мы получаем удивительно простой формула:
D_ij * p_j - p_j * p_i
если вы действительно хотите, мы можем разделить его на i = j и i != j случаях:
i = j: D_ii * p_i - p_i * p_i = p_i - p_i * p_i = p_i * (1 - p_i)
i != j: D_ij * p_i - p_i * p_j = -p_i * p_j
это наш ответ.
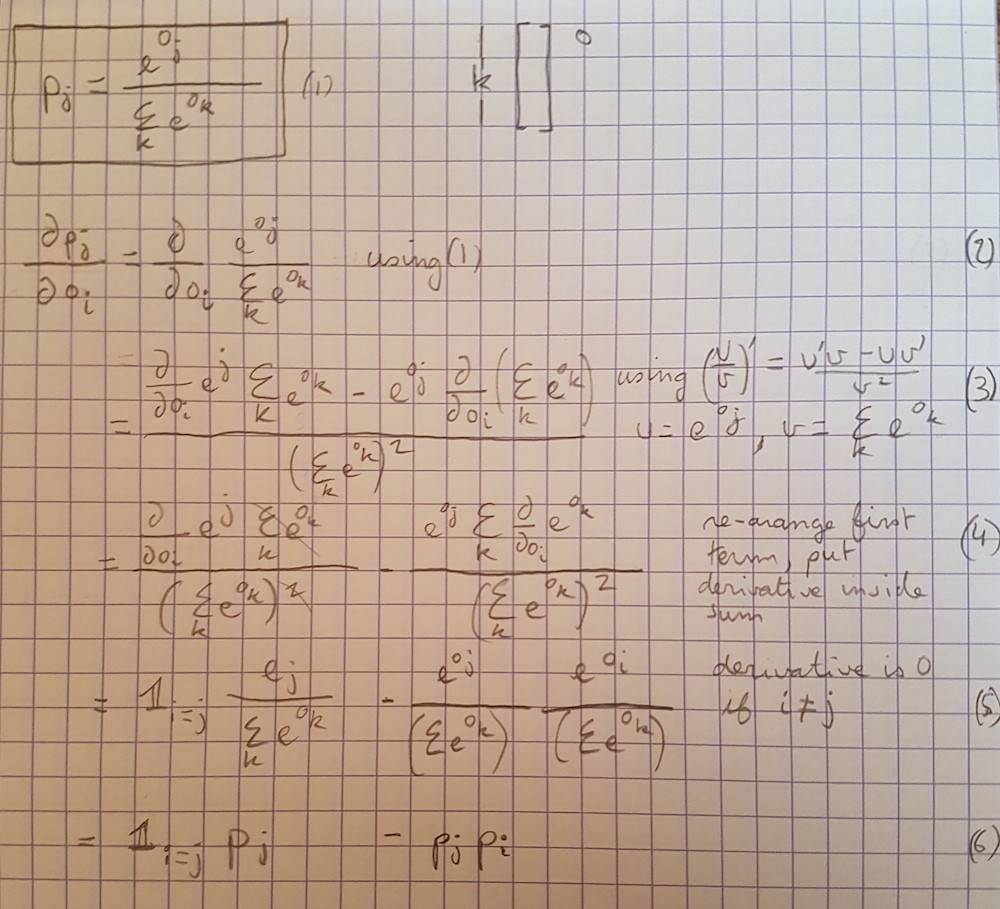
для чего это стоит, вот мой вывод, основанный на ответе SirGuy: (не стесняйтесь указывать ошибки, если вы их найдете).