Расчет градиента с помощью python
Я хотел бы знать, каким образом numpy.gradient работа.
Я использовал градиент, чтобы попытаться вычислить групповая скорость (групповая скорость волнового пакета является производной частот по отношению к волновым числам, а не группой скоростей). Я подал ему массив из 3 столбцов, первые 2 colums-это X и y coords,третий столбец-частота этой точки (x, y). Мне нужно вычислить градиент, и я ожидал 2d-вектор, являющийся определением градиента
df/dx*i+df/dy*j+df/dz*k
и моя функция только функция x и y я ожидал чего-то вроде
df/dx*i+df/dy*j
но я получил 2 массива с 3 колумами каждый, т. е. 2 3d вектора; сначала я думал, что сумма двух даст мне вектор, который я искал, но компонент z не исчезает. Надеюсь, я достаточно ясно объяснил. Я хотел бы знать, как numpy.gradient работает, и если это правильный выбор для моей проблемы. В противном случае я хотел бы знать, есть ли какая-либо другая функция python, которую я могу использовать.
Я имею в виду: я хочу вычислить градиент массива значений:
data=[[x1,x2,x3]...[x1,x2,x3]]
где x1, x2-координаты точек на равномерной сетке (мои точки в зоне бриллюэна), а x3-значение частоты для этой точки. Я даю в вводе также шаги для вывода для 2 направлений:
stepx=abs(max(unique(data[:,0])-min(unique(data[:,0]))/(len(unique(data[:,0]))-1)
то же самое для y-направлении. Я не строил свои данные на сетке, у меня уже есть сетка, и поэтому добрые примеры, приведенные здесь в ответах, мне не помогают. Более подходящий пример должен иметь сетку точек и значений, как у меня:
data=[]
for i in range(10):
for j in range(10):
data.append([i,j,i**2+j**2])
data=array(data,dtype=float)
gx,gy=gradient(data)
еще одна вещь, которую я могу добавить, это то, что моя сетка не квадратная, а имеет форму многоугольника, являющегося зоной бриллюэна 2d-кристалла.
я понял, что numpy.gradient работает правильно только на квадратной сетке значений, а не то, что я ищу. Даже если я сделаю свои данные в виде сетки, которая будет иметь много нулей за пределами полигона моих исходных данных, это добавит действительно высокие векторы моего градиента влияют (отрицательно) на точность вычисления. Этот модуль кажется мне скорее игрушкой, чем инструментом, он имеет серьезные ограничения imho.
проблема решена с помощью словарей.
1 ответов
вам нужно дать gradient матрица, которая описывает ваши значения угловой частоты для вашего (x,y) очков. например,
def f(x,y):
return np.sin((x + y))
x = y = np.arange(-5, 5, 0.05)
X, Y = np.meshgrid(x, y)
zs = np.array([f(x,y) for x,y in zip(np.ravel(X), np.ravel(Y))])
Z = zs.reshape(X.shape)
gx,gy = np.gradient(Z,0.05,0.05)
вы можете видеть, что построение Z как поверхность дает:
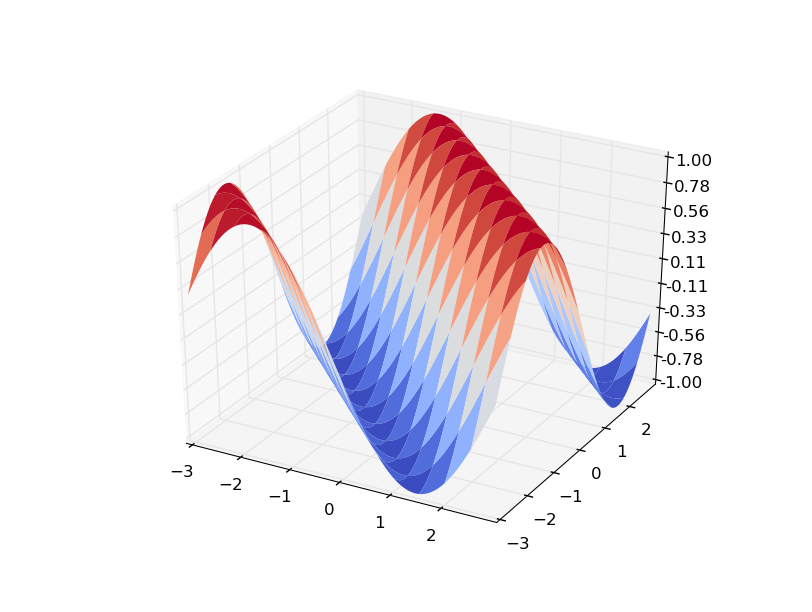
вот как интерпретировать ваш градиент:
gx - это матрица, которая дает изменение dz/dx по всем пунктам. например, gx[0][0] is dz/dx at (x0,y0). Визуализация gx помогает в понимание:
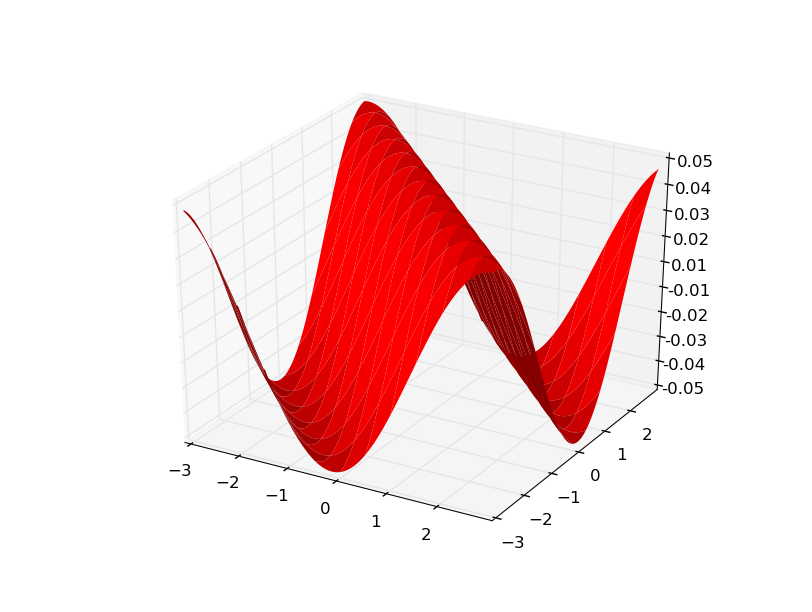
так как мои данные были сгенерированы из f(x,y) = sin(x+y) gy выглядит так же.
вот более очевидный пример использования f(x,y) = sin(x)...
f (x,y)
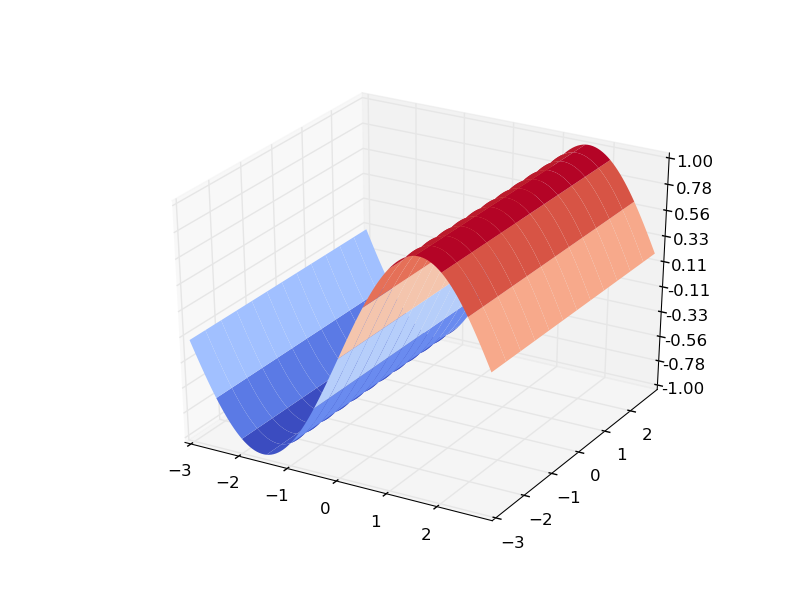
и градиентов
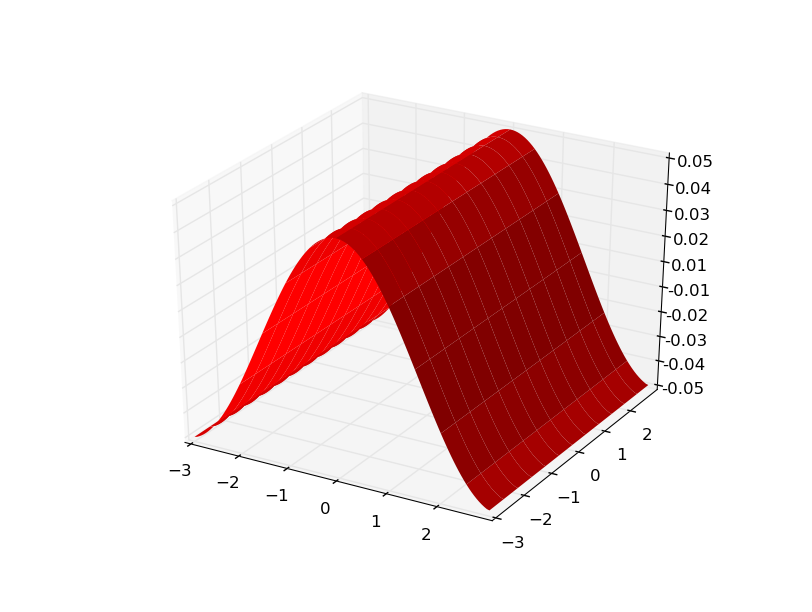
обновление давайте взглянем на пары xy.
это код I используется:
def f(x,y):
return np.sin(x)
x = y = np.arange(-3,3,.05)
X, Y = np.meshgrid(x, y)
zs = np.array([f(x,y) for x,y in zip(np.ravel(X), np.ravel(Y))])
xy_pairs = np.array([str(x)+','+str(y) for x,y in zip(np.ravel(X), np.ravel(Y))])
Z = zs.reshape(X.shape)
xy_pairs = xy_pairs.reshape(X.shape)
gy,gx = np.gradient(Z,.05,.05)
теперь мы можем посмотреть и увидеть, что именно происходит. Скажем, мы хотели знать, какая точка связана со значением atZ[20][30]? Затем...
>>> Z[20][30]
-0.99749498660405478
и
>>> xy_pairs[20][30]
'-1.5,-2.0'
это верно? Давай проверим.
>>> np.sin(-1.5)
-0.99749498660405445
да.
и каковы наши градиентные компоненты в этой точке?
>>> gy[20][30]
0.0
>>> gx[20][30]
0.070707731517679617
они проверяют?
dz/dy always 0 проверка.
dz/dx = cos(x) и...
>>> np.cos(-1.5)
0.070737201667702906
выглядит хорошо.
вы заметите, что они не совсем верны, потому что мои данные Z не непрерывны, есть размер шага 0.05 и gradient можно только приблизить скорость изменения.
