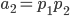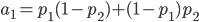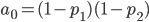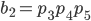Расчета вероятности отказа системы в распределенной сети
Я пытаюсь построить математическую модель в наличии файла в распределенной файловой системе. Я разместил этот вопрос в MathOverflow, но это также может быть классифицировано как CS-вопрос, поэтому я даю ему шанс здесь.
система работает следующим образом: узел хранит файл (encoed с использованием кодов стирания) на R*B удаленных узлах, где r-коэффициент репликации, А b-целочисленная константа. Файлы с кодом стирания имеют свойство, что файл может быть восстановлен iff в минимум b удаленных узлов доступны и возвращают свою часть файла.
самый простой подход к этому-предположить, что все удаленные узлы независимы друг от друга и имеют одинаковую доступность p. При этих предположениях доступность файла следует за Биномиальным распределением, т. е. биномиальное распределение http://bit.ly/dyJwwE
к сожалению, эти два предположения могут ввести недопустимую ошибку, как показано в этой статье: http://deim.urv.cat/~Луисе.pamies/загрузки/Главная/icpp09-бумаги.формат PDF.
=B доступными узлами. Этот подход является более правильным, но имеет вычислительную стоимость ОРДО http://bit.ly/cEZcAP. Кроме того, он не имеет дело с предположением о независимости узла.у вас есть идеи хорошего приближения, которое вводит меньше ошибок, чем биномиальное распределение-апроксимация, но с лучшим вычислительная стоимость, чем http://bit.ly/d52MM9 http://bit.ly/cEZcAP?
вы можете предположить, что данные доступности каждого узла представляют собой набор кортежей, состоящий из (measurement-date, node measuring, node being measured, succes/failure-bit). С помощью этих данных можно, например, вычислить корреляцию доступности между узлами и дисперсией доступности.
2 ответов
большие r и b вы можете использовать метод, называемый интеграцией Монте-Карло, см., например,интеграция Монте-Карло в Википедии (и/или глава 3.1.2 SICP) для вычисления суммы. Для малых r и b и значительно разные вероятности отказа узла p[i] точный метод превосходит. Точное определение маленький и большой будет зависеть от нескольких факторов и лучше опробовали экспериментально.
конкретный пример кода: это очень простой пример кода (в Python), чтобы продемонстрировать, как такая процедура может работать:
def montecarlo(p, rb, N):
"""Corresponds to the binomial coefficient formula."""
import random
succ = 0
# Run N samples
for i in xrange(N):
# Generate a single test case
alivenum = 0
for j in xrange(rb):
if random.random()<p: alivenum += 1
# If the test case succeeds, increase succ
if alivenum >= b: succ += 1
# The final result is the number of successful cases/number of total cases
# (I.e., a probability between 0 and 1)
return float(succ)/N
функция соответствует биномиальному тестовому набору и выполняется N тесты, проверки, если b узлы из r*b узлы живы с вероятностью отказа p. Несколько экспериментов убедят вас, что вам нужны значения N в пределах тысячи образцов, прежде чем вы можете получите любые разумные результаты, но в принципе сложность есть O(N*r*b). Точность результата масштабируется как sqrt(N), то есть, чтобы увеличить точность в два раза, вам нужно увеличить N в четыре раза. Для достаточно больших r*b этот метод будет явно превосходит.
расширение приближения: очевидно, вам нужно разработать тестовый случай таким образом, чтобы он уважал все свойства системы. Вы предложили пару расширения, некоторые из которых могут быть легко реализованы, а другие-нет. Позвольте мне дать вам несколько советов:
1) в случае различных, но некоррелированных p[i], изменения вышеуказанного кода минимальны: в функциональной головке вы передаете массив вместо одного float p и вы замените строку if random.random()<p: alivenum += 1 by
if random.random()<p[j]: alivenum += 1
2) в случае коррелированных p[i] вам нужна дополнительная информация о системе. Ситуация я имел в виду в мой комментарий может быть такой сетью:
A--B--C
| |
D E
|
F--G--H
|
J
в этом случае A может быть "корневой узел" и сбой узла D может означать автоматический отказ со 100% вероятностью узлов F, G, H и J; в то время как сбой узла F автоматически сбил бы G, H и J etc. По крайней мере, это был тот случай, о котором я говорил в своем комментарии (что является правдоподобной интерпретацией, так как вы говорите о дереве структура вероятностей в исходном вопросе). В такой ситуации вам нужно будет изменить код, который p относится к древовидной структуре и for j in ... обходит дерево, пропуская нижние ветви из текущего узла, как только тест завершается неудачно. Полученный тест по-прежнему является ли alivenum >= b как и раньше, конечно.
3) Этот подход потерпит неудачу, если сеть представляет собой циклический граф, который не может быть представлен древовидной структурой. В таком случае вам нужно сначала создать график узлы, которые либо мертвы, либо живы, а затем запустить алгоритм маршрутизации на графике, чтобы подсчитать количество уникальных, достижимых узлов. Это не увеличит временную сложность алгоритма, но, очевидно, сложность кода.
4) зависимость от времени является нетривиальной, но возможной модификацией, если вы знаете m.т. b.f/r (среднее время между отказами / ремонтами), так как это может дать вам вероятности p древовидной структуры или некоррелированной линейной p[i] в сумме экспоненты. Затем вам придется запускать MC-процедуру в разное время с соответствующими результатами для p.
5) Если у вас есть только файлы журнала (как указано в вашем последнем абзаце), это потребует существенной модификации подхода, который выходит за рамки того, что я могу сделать на этой доске. Лог-файлы должны быть достаточно подробными, чтобы позволить восстановить модель сетевого графика (и, следовательно, график p), а также индивидуальные значения всех узлы p. Иначе точность была бы ненадежной. Эти лог-файлы также должны быть значительно длиннее, чем временные рамки сбоев и ремонтов, что может быть нереалистичным в реальных сетях.
предполагая, что каждый узел имеет постоянную, известную и независимую скорость доступности, на ум приходит подход "разделяй и властвуй".
скажите, что у вас есть N узлы.
- разделить их на две группы
N/2узлы. - для каждой стороны, вычислить вероятность того, что любое количество узлов (
[0,N/2]) вниз. - умножьте и суммируйте их по мере необходимости, чтобы найти вероятность того, что любое число (
[0,N]) полный комплект вниз.
Шаг 2 можно сделать рекурсивно, и на верхнем уровне вы можете суммировать, как нужно, чтобы найти, как часто больше, чем некоторое число вниз.
Я не знаю сложности этого, но если я должен угадать, я бы сказал, На или ниже O(n^2 log n)
механику этого можно проиллюстрировать на терминальном корпусе. Скажем, у нас есть 5 узлов с up times 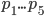
A С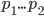
B С 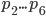
Для A:
Для B:
окончательные результаты для этого этапа можно найти путем умножения каждого из aС каждого bи суммирование соответствующим образом.
v[0] = a[0]*b[0]
v[1] = a[1]*b[0] + a[0]*b[1]
v[2] = a[2]*b[0] + a[1]*b[1] + a[0]*b[2]
v[3] = a[2]*b[1] + a[1]*b[2] + a[0]*b[3]
v[4] = a[2]*b[2] + a[1]*b[3]
v[5] = a[2]*b[3]