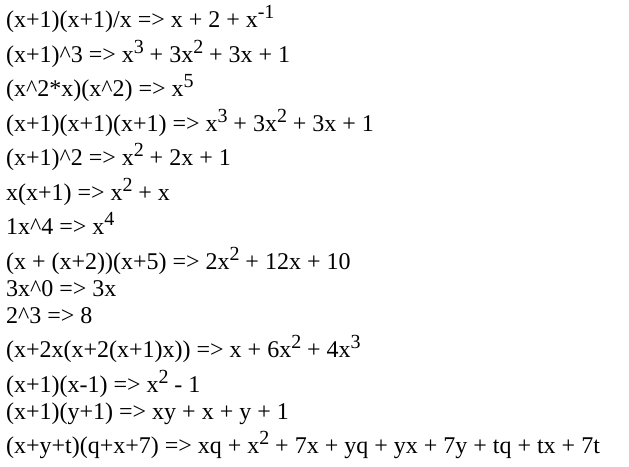Разложение алгебраического члена

Edit: я переписал свой первоначальный ответ, когда вопрос не включал - и / операторы). Мой новый ответ поддерживает - и /.

поскольку вы не определили точную грамматику, я сделал некоторые предположения. Я поддерживаю +, -, /, ^ операторы и неявное умножение. Они могут оперировать числами,x и (...) выражения, за исключением правой стороны ^ оператор должно быть числом. Я разрешаю пробелы между токенами.

Ограничения:-бинарный не унарный - оператор, So x-2 если ОК -2 сама по себе является синтаксической ошибкой. The / ограничено. Вы можете разделить на значение с одним коэффициентом, таким как 2, 'x',2x^2, но не может иметь 1/(x^2+1), который будет оценивать бесконечный ряд.

сначала он берет строку и обертывает ее в "токенизатор" , который позволяет вам смотреть на один токен на время, где токен-это число,x, ( ) или оператора.

затем он называет evaluateSum(), который оценивает вещи, разделенные + или -, где каждая вещь является продуктом, оцениваемым evaluateProduct(). Это в свою очередь использует evaluatePower() в evalue в ^. Наконец evaluateTerm() ищет x, цифры и скобки подвыражения, которые оцениваются рекурсивно с evaluateSum(). Эта иерархия создает правильный приоритет и оценку оператора порядок.

каждый слой оценки возвращает объект "коэффициенты", который похож на массив, но может содержать мегативные индексы. Например [1,0,1] означает 1+x^2.

он может справиться с любым количеством вложенных скобок и много других дел, таких как xx(x) is x^3, 2^3 is 8. Я добавил несколько бросков для синтаксических ошибок, например 2^x является незаконным.

function makeTokenizer(source) {
    var c, i, tokenizer;
    i = 0; // The index of the current character.
    c = source.charAt(i); // The current character.
    function consumeChar() { // Move to next c, return previous c.
        var prevC = c;
        i += 1;
        c = source.charAt(i);
        return prevC;
    }
    tokenizer = {
        next : function () {
            var str;
            while (c === ' ') { // Skip spaces
                consumeChar();
            }
            if (!c) {
                tokenizer.token = undefined; // End of source
            } else if (c >= '0' && c <= '9') { // number
                str = consumeChar(); // First digit
                while (c >= '0' && c <= '9') { // Look for more digits.
                    str += consumeChar();
                }
                tokenizer.token = Number(str);
            } else if (c === "x") {
                tokenizer.token = consumeChar();
            } else { // single-character operator
                tokenizer.token = consumeChar();
            }
        }
    };
    tokenizer.next(); // Load first token.
    return tokenizer;
}
function makeCoefficients() { // Make like an array but can have -ve indexes
    var min = 0, max = 0, c = {};
    return {
        get: function (i) {
            return c[i] || 0;
        },
        set: function (i, value) {
            c[i] = value;
            min = Math.min(i, min);
            max = Math.max(i + 1, max);
            return this; // for chaining
        },
        forEach: function (callback) {
            var i;
            for (i = min; i < max; i += 1) {
                if (this.get(i)) {
                    callback(this.get(i), i);
                }
            }
        },
        toString: function () {
            var result = "", first = true;
            this.forEach(function (val, power) {
                result += (val < 0 || first) ? "" : "+";
                first = false;
                result += (val === 1 && power !== 0) ? "" : val;
                if (power) {
                    result += "x";
                    if (power !== 1) {
                        result += "^" + power;
                    }
                }
            });
            return result;
        },
        toPowerOf: function (power) {
            if (power === 0) {
                return makeCoefficients().set(0, 1); // Anything ^0 = 1
            }
            if (power === 1) {
                return this;
            }
            if (power < 0) {
                throw "cannot raise to negative powers";
            }
            return this.multiply(this.toPowerOf(power - 1));
        },
        multiply: function (coefficients) {
            var result = makeCoefficients();
            this.forEach(function (a, i) {
                coefficients.forEach(function (b, j) {
                    result.set(i + j, result.get(i + j) + a * b);
                });
            });
            return result;
        },
        divide: function (coefficients) {
            // Division is hard, for example we cannot do infinite series like:
            // 1/(1 + x^2) = sum_(n=0 to infinity) 1/2 x^n ((-i)^n + i^n)
            // So we do a few easy cases only.
            var that = this, result = makeCoefficients(), done;
            coefficients.forEach(function (value, pow) {
                that.forEach(function (value2, pow2) {
                    result.set(pow2 - pow, value2 / value);
                });
                if (done) {
                    throw "cannot divide by " + coefficients.toString();
                }
                done = true;
            });
            return result;
        },
        add: function (coefficients, op) {
            var result = makeCoefficients();
            this.forEach(function (value, i) {
                result.set(value, i);
            });
            op = (op === "-" ? -1 : 1);
            coefficients.forEach(function (value, i) {
                result.set(i, result.get(i) + value * op);
            });
            return result;
        }
    };
}
var evaluateSum; // Called recursively
function evaluateTerm(tokenizer) {
    var result;
    if (tokenizer.token === "(") {
        tokenizer.next();
        result = evaluateSum(tokenizer);
        if (tokenizer.token !== ")") {
            throw ") missing";
        }
        tokenizer.next();
    } else if (typeof tokenizer.token === "number") {
        result = makeCoefficients().set(0, tokenizer.token);
        tokenizer.next();
    } else if (tokenizer.token === "x") {
        tokenizer.next();
        result = makeCoefficients().set(1, 1); // x^1
    } else {
        return false; // Not a 'term'
    }
    return result;
}
function evaluatePower(tokenizer) {
    var result;
    result = evaluateTerm(tokenizer);
    if (tokenizer.token === "^") {
        tokenizer.next();
        if (typeof tokenizer.token !== "number") {
            throw "number expected after ^";
        }
        result = result.toPowerOf(tokenizer.token);
        tokenizer.next();
    }
    return result;
}
function evaluateProduct(tokenizer) {
    var result, term, divOp;
    result = evaluatePower(tokenizer);
    if (!result) {
        throw "Term not found";
    }
    while (true) {
        divOp = (tokenizer.token === "/");
        if (divOp) {
            tokenizer.next();
            term = evaluatePower(tokenizer);
            result = result.divide(term);
        } else {
            term = evaluatePower(tokenizer);
            if (!term) {
                break;
            }
            result = result.multiply(term);
        }
    }
    return result;
}
function evaluateSum(tokenizer) {
    var result, op;
    result = evaluateProduct(tokenizer);
    while (tokenizer.token === "+" || tokenizer.token === "-") {
        op = tokenizer.token;
        tokenizer.next();
        result = result.add(evaluateProduct(tokenizer), op);
    }
    return result;
}

function evaluate(source) {
    var tokenizer = makeTokenizer(source),
        coefficients = evaluateSum(tokenizer);
    if (tokenizer.token) {
        throw "Unexpected token " + tokenizer.token;
    }
    console.log(source + " => " + coefficients.toString());
}

// Examples:
evaluate("(x+1)(x+1)"); // => 1+2x+x^2
evaluate("(x+1)^2"); // => 1+2x+x^2
evaluate("(x+1)(x+1)(x+1)"); // => 1+3x+3x^2+x^3
evaluate("(x+1)^3"); // => 1+3x+3x^2+x^3
evaluate("(x)(x+1)"); // => x+x^2
evaluate("(x+1)(x)"); // => x+x^2
evaluate("3x^0"); // => 3
evaluate("2^3"); // => 8
evaluate("(x+2x(x+2(x+1)x))"); // => x+6x^2+4x^3
evaluate("(x+1)(x-1)"); // => -1+x^2
evaluate("(x+1)(x+1)/x"); // x^-1+2+x
//evaluate("(x+1)/(x^2 + 1)"); //throws  cannot divide by 1+2x

мой подход использует два вспомогательных класса:

-Term: здесь хранятся коэффициент и объект, ключами которых являются переменные, а значениями-экспоненты. Он имеет методы определения того, являются ли члены "одинаковыми" (т. е. имеют ли они одинаковые переменные с одинаковыми показателями, что позволяет их добавлять), добавлять термины и умножать термины. -Polynomial: это хранит массив терминов. Имеет методы сложения двух полиномов, умножения двух многочлены и упрощающие многочлены (исключая члены с 0 коэффициентами и комбинируя подобные члены).

он имеет две существенные вспомогательные функции: -findOuterParens - учитывая строку, эта функция возвращает индексы первой внешней пары левых и правых скобок. -parseExpressionStr - эта функция использует регулярное выражение для разделения строки на три типа подстрок: 1) число, 2) символ (т. е. переменная, например " x " или "y") или 3) оператор (*, -, +, ^, /). Он создает Polynomial объекты для первых двух типов и оставляет операторы в виде строк.

на expand функция запускает шоу. Он принимает строку и возвращает Polynomial объект, представляющий расширенную форму многочлена в строке. Он делает это следующим образом: 1) он имеет дело с круглыми скобками рекурсией. Он использует findOuterParens найти все внешний parenthsized подстрок. Таким образом, для "3x*(x+4)+(2(y+1))*t", например, он найдет "x+4" и "2(y+1)" в скобках подстроки. Это тогда передает их себе для дальнейшего анализа. Для "2 (y+1)" он идентифицирует "y+1" Как скобочную подстроку и передает это себе для трех уровней рекурсии для этого примера. 2) он имеет дело с другими частями строки, используя parseExpressionStr. После шагов 1 и 2 он имеет массив, содержащий полиномиальные объекты и операторы (хранящиеся в виде строк). Затем он переходит к упрощению и расширению. 3) он преобразует подзадачи вычитания в подзадачи сложения, заменяя все - 's на +' s и умножение всех многочленов, следующих за- ' s на -1. 4) он преобразует подзадачи деления в подзадачи умножения путем замены /'s на *'s и инвертирования Polynomial после /. Если многочлен, следующий за/, имеет более одного члена, он выдает ошибку. 5) он преобразует подзадачи мощности в подзадачи умножения, заменяя ^на ряд умножения. 6) он добавляет в implicit *. Т. е. если два полиномиальных элемента находятся рядом друг с другом в массиве, то это выводится что они умножаются, так, например, '2*x' = = '2x'. 7) Теперь массив имеет полиномиальные объекты, чередующиеся с " + "или"*". Сначала он выполняет все полиномиальные умножения, а затем выполняет все дополнения. 8) он выполняет заключительный шаг упрощения и возвращает полученный расширенный многочлен.

<html>
<head></head>
<body></body>
<script>

function findOuterParens(str) {
	var leftIndex = str.indexOf('('), leftNum = 1, rightNum = 0;

	if (leftIndex === -1)
		return

	for (var i=leftIndex+1; i<str.length; i++) {
		if (str[i] === '(')
			leftNum++;
		else if (str[i] === ')')
			rightNum++, rightIndex=i;
		if (leftNum === rightNum)
			return {start: leftIndex, end: rightIndex}
	}

	throw Error('Parenthesis at position ' + leftIndex + ' of "' + str + '" is unpaired.');
}

function parseExpressionStr(inputString) {
	var result = [], str = inputString;
	while (str) {
		var nextPart = str.match(/([\d]+)|([\+\-\^\*\/])|([a-zA-z])/);
		if (!nextPart)
			return result;
		if (nextPart.length === 0)
			throw Error('Unable to parse expression string "' + inputString + '". Remainder "' + str + '" could not be parsed.');
		else if (nextPart[1])					// First group (digits) matched
			result.push(new Polynomial(parseFloat(nextPart[0])));
		else if (nextPart[3])					// Third group (symbol) matched
			result.push(new Polynomial(nextPart[0]));
		else									// Second group (operator) matched
			result.push(nextPart[0]);
		str = str.substring(nextPart.index+nextPart[0].length);
	}
	return result
}

function isOperator(char) {
	return char === '*' || char === '/' || char === '^' || char === '+' || char === '-';
}


function Polynomial(value) {
	this.terms = (value!==undefined) ? [new Term(value)] : [];
}

Polynomial.prototype.simplify = function() {
	for (var i=0; i<this.terms.length-1; i++) {
		if (this.terms[i].coeff === 0) {
			this.terms.splice(i--, 1);
			continue;
		}
		for (var j=i+1; j<this.terms.length; j++) {
			if (Term.same(this.terms[i], this.terms[j])) {
				this.terms[i] = Term.add(this.terms[i], this.terms[j]);
				this.terms.splice(j--, 1);
			}
		}
	}
}

Polynomial.add = function(a, b) {
	var result = new Polynomial();
	result.terms = a.terms.concat(b.terms);
	result.simplify();
	return result
}

Polynomial.multiply = function(a, b) {
	var result = new Polynomial();
	a.terms.forEach(function(aTerm) {
		b.terms.forEach(function (bTerm) {
			result.terms.push(Term.multiply(aTerm, bTerm));
		});
	});
	result.simplify();

	return result
}

Polynomial.prototype.toHtml = function() {
	var html = ''
	for (var i=0; i<this.terms.length; i++) {
		var term = this.terms[i];
		if (i !== 0)
			html += (term.coeff < 0) ? ' - ' : ' + ';
		else
			html += (term.coeff < 0) ? '-' : '';
		var coeff = Math.abs(term.coeff);
		html += (coeff === 1 && Object.keys(term.symbols).length > 0) ? '' : coeff;

		for (var symbol in term.symbols) {
			var exp = term.symbols[symbol];
			exp = (exp !== 1) ? exp : '';
			html += symbol + '<sup>' + exp + '</sup>';
		}
	}
	return html;
}

function Term(value) {
	this.symbols = {};
	if (typeof value==='string') {			// Symbol
		this.symbols[value] = 1;
		this.coeff = 1;
	} else if (typeof value==='number') {	// Number
		this.coeff = value;
	} else {
		this.coeff = 1;
	}
}

Term.same = function(a, b) {
	if (Object.keys(a.symbols).length != Object.keys(b.symbols).length)
		return false
	else
		for (var aSymbol in a.symbols)
			if (a.symbols[aSymbol] != b.symbols[aSymbol]) return false
	return true
}

Term.add = function(a, b) {
	var result = new Term();
	Object.assign(result.symbols, a.symbols);
	result.coeff = a.coeff + b.coeff;
	return result
}

Term.multiply = function(a, b) {
	var result = new Term();
	Object.assign(result.symbols, a.symbols);
	for (var symbol in b.symbols) {
		if (!(symbol in result.symbols))
			result.symbols[symbol] = 0;
		result.symbols[symbol] += b.symbols[symbol];
		if (result.symbols[symbol] === 0)
			delete result.symbols[symbol];
	}
	result.coeff = a.coeff * b.coeff;
	return result
}

function expand(str) {
	var result = [];

	var parens = findOuterParens(str);
	while (parens) {
		result = result.concat(parseExpressionStr(str.slice(0,parens.start)));
		result.push(expand(str.slice(parens.start+1, parens.end)))
		str = str.slice(parens.end+1);
		parens = findOuterParens(str);
	} 
	result = result.concat(parseExpressionStr(str));

	// Move -s to coefficients
	var minus = result.indexOf('-'), minusPoly = new Polynomial(-1);
	while (minus !== -1) {
		result[minus] = '+';
		result[minus+1] = Polynomial.multiply(minusPoly, result[minus+1]);
		minus = result.indexOf('-');
	}

	// Get rid of +s that follow another operator
	var plus = result.indexOf('+');
	while (plus !== -1) {
		if (plus===0 || isOperator(result[plus-1])) {
			result.splice(plus--, 1);
		}
		plus = result.indexOf('+', plus+1);
	}

	// Convert /s to *s
	var divide = result.indexOf('/');
	while (divide !== -1) {
		result[divide] = '*';
		var termsToInvert = result[divide+1].terms;
		if (termsToInvert.length > 1)
			throw Error('Attempt to divide by a polynomial with more than one term.');
		var termToInvert = termsToInvert[0];
		for (var symbol in termToInvert.symbols) {
			termToInvert.symbols[symbol] = -termToInvert.symbols[symbol];
		}
		termToInvert.coeff = 1/termToInvert.coeff;
		divide = result.indexOf('/');
	}

	// Convert ^s to *s
	var power = result.indexOf('^');
	while (power !== -1) {
		var exp = result[power+1];
		if (exp.terms.length > 1 || Object.keys(exp.terms[0].symbols).length != 0)
			throw Error('Attempt to use non-number as an exponent');
		exp = exp.terms[0].coeff;
		var base = result[power-1];
		var expanded = [power-1, 3, base];
		for (var i=0; i<exp-1; i++) {
			expanded.push('*');
			expanded.push(base);
		}
		result.splice.apply(result, expanded);
		power = result.indexOf('^');
	}

	// Add implicit *s
	for (var i=0; i<result.length-1; i++)
		if (!isOperator(result[i]) && !(isOperator(result[i+1])))
			result.splice(i+1, 0, '*');

	// Multiply
	var mult = result.indexOf('*');
	while (mult !== -1) {
		var product = Polynomial.multiply(result[mult-1], result[mult+1]);
		result.splice(mult-1, 3, product);
		mult = result.indexOf('*');
	}

	// Add
	var add = result.indexOf('+');
	while (add !== -1) {
		var sum = Polynomial.add(result[add-1], result[add+1]);
		result.splice(add-1, 3, sum);
		add = result.indexOf('+');
	}

	result[0].simplify();
	return result[0];
}

var problems = ['(x+1)(x+1)/x', '(x+1)^3', '(x^2*x)(x^2)', '(x+1)(x+1)(x+1)',
				'(x+1)^2', 'x(x+1)', '1x^4', '(x + (x+2))(x+5)', '3x^0', '2^3',
				'(x+2x(x+2(x+1)x))', '(x+1)(x-1)', '(x+1)(y+1)', '(x+y+t)(q+x+7)'];

var solutionHTML = '';
for (var i = 0; i<problems.length; i++) {
	solutionHTML += problems[i] + '    =>    ' + expand(problems[i]).toHtml() + '<br>';
}
document.body.innerHTML = solutionHTML;


</script>
</html>

он выводит: