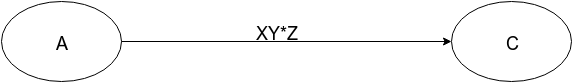Регулярное выражение для двоичных чисел, кратных 5
Я хочу написать регулярное выражение для двоичных чисел, кратных 5.
Я уже сделал регулярные выражения для двоичных чисел, делимых на 2 и 3, но я не мог найти один для 5.
какие предложения?
3 ответов
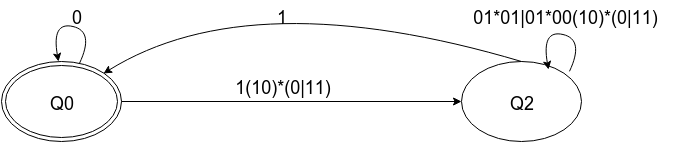
(0|1(10)*(0|11)(01*01|01*00(10)*(0|11))*1)*
добавить ^$ чтобы проверить его с помощью regexp. это здесь.
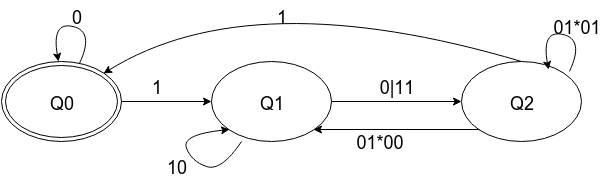
Вы можете построить DFA и преобразовать его в регулярное выражение. DFA уже был построен в еще один ответ. Вы можете прочитать это, это очень хорошо объяснено.
Общая идея состоит в том, чтобы удалить узлы, добавив ребра.
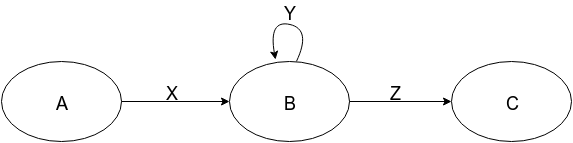
будет:
Использование этого преобразования и DFA из ответа, который я связал, вот шаги, чтобы получить регулярное выражение:
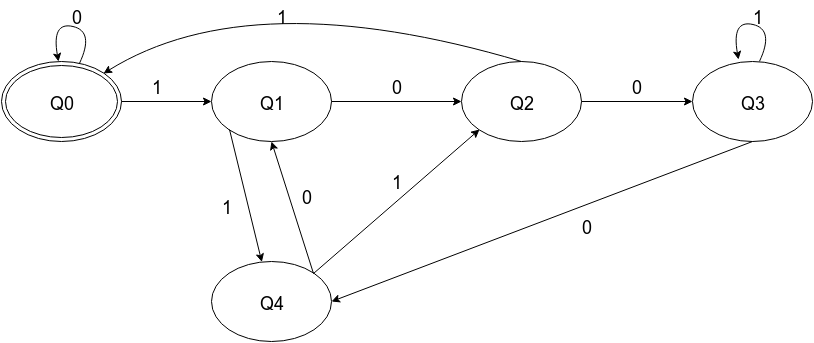
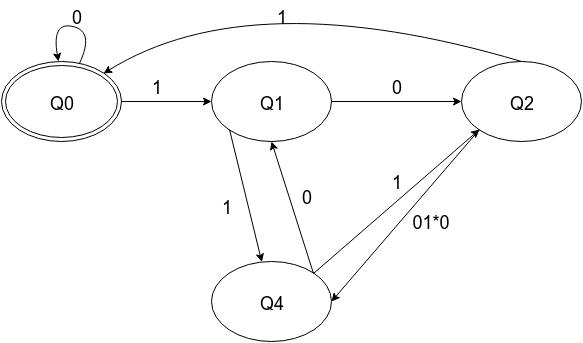

2^0 = 1 = 1 mod 5
2^1 = 2 = 2 mod 5
2^2 = 4 = -1 mod 5
2^3 = 8 = -2 mod 5
2^4 = 16 = 1 mod 5
2^5 = 32 = 2 mod 5
... -1 mod 5
... -2 mod 5
таким образом, у нас есть шаблон 1, 2, -1, -2. Есть два подзаголовка, где чередуется только знак числа: пусть n цифра и количество наименее значащая цифра 0; нечетный шаблон
(-1)^(n)
и даже шаблон
2x((-1)^(n))
Итак, как это использовать?
пусть исходное число будет 100011, разделите цифры чисел на две части, четные и нечетные. Суммируйте цифры каждой части отдельно. Умножить сумму нечетных цифры на 2. Теперь, если результат делится на сумму четных цифр, то исходное число делится на 5, то оно не делится. Пример:
100011
1_0_1_ 1+0+1 = 2
_0_0_1 0+0+1 = 1; 1x2 = 2
2 mod(2) equals 0? Yes. Therefore, original number is divisible.
как применить его в регулярном выражении? Используя обозначение функции в регулярном выражении он может быть применен. Выноски предоставляют средство временной передачи управления сценарию в середине сопоставления шаблонов регулярных выражений.
однако ответ ndn более уместен и проще, поэтому я рекомендую воспользоваться его ответом.