Шаги по созданию NFA из регулярного выражения
У меня возникли проблемы с описанием каждого шага при создании НКА из регулярного выражения. Вопрос заключается в следующем:
преобразуйте следующее регулярное выражение в недетерминированный конечный автомат (NFA), четко описывающий шаги используемого алгоритма: (b|a)*b(a / b)
Я сделал простую машину 3-го состояния, но это очень много от интуиции. Это вопрос из прошлого экзамена, написанного моим лектором, который также написал следующее объяснение алгоритма Томпсона:http://www.cs.may.ie/staff/jpower/Courses/Previous/parsing/node5.html
может ли кто-нибудь прояснить, как "четко описать каждый шаг"? Это просто кажется набором основных правил, а не алгоритмом с шагами, которым нужно следовать.
может быть, есть алгоритм, который я где-то замазал, но до сих пор я только что создал их с обоснованной догадкой.
2 ответов
краткая версия для общего подхода.
Там есть Альго, называемый алгоритмом построения Томпсона-Макнотона-Ямады, или иногда просто "Томпсон Констракшн"."Строятся промежуточные NFAs, заполняя куски по пути, соблюдая приоритет оператора: сначала круглые скобки, затем Kleene Star (например, a*), затем конкатенация (например, ab), а затем чередование (например, a|b).
вот подробное пошаговое руководство для построения (b|a)*b(a / b)'S NFA
строительство верхнего уровня
ручки скобки. Примечание: в фактической реализации, это может иметь смысл для обработки круглых скобках через рекурсивный вызов на их содержание. Для ясности, я отложу оценку чего-либо внутри родителей.
Kleene Stars: только один * там, поэтому мы строим заполнитель Kleene Star machine под названием P (который позже будет содержать b|a). Промежуточный результат:
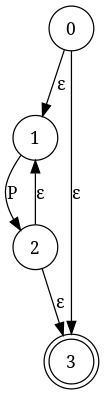
конкатенация: присоедините P к b и присоедините b к машине-заполнителю Q (которая будет содержать (a|b). Промежуточный результат:

нет чередования вне скобок, поэтому мы пропустим это.
теперь мы сидим на машине P*bQ. (Обратите внимание, что наши заполнители P и Q-это просто машины конкатенации.) Мы заменяем край P на NFA для b / a и заменяем Q edge с NFA для a / b через рекурсивное применение вышеуказанных шагов.
Здание P
пропустить. Нет фаренс.
пропустить. Никаких звезд Клина.
пропустить. Нет contatenation.
Построьте машину перемежения для Б/ А. Промежуточный результат:
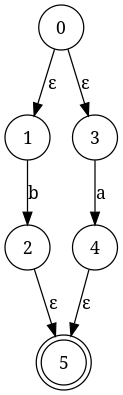
интеграция P
затем мы возвращаемся к этой машине P*bQ и вырываем край P. У нас есть источник края P служить в качестве начального состояния для машины P и назначение края P служить государству местом для машины. Мы также заставляем это государство отвергать (отбирать его свойство быть принимающим государством). Результат выглядит так:
дом Q
пропустить. Нет фаренс.
пропустить. Никаких звезд Клина.
пропустить. Нет contatenation.
Построьте машину перемежения для a / b. Кстати, чередование коммутативно, поэтому a|b логически эквивалентно b|A. (Читайте: пропуская эту небольшую диаграмму сноски из лени.)
Интеграция Q
мы делаем то, что мы сделали с P выше, за исключением замены края Q на intermedtae B|A машину, которую мы построили. Вот результат: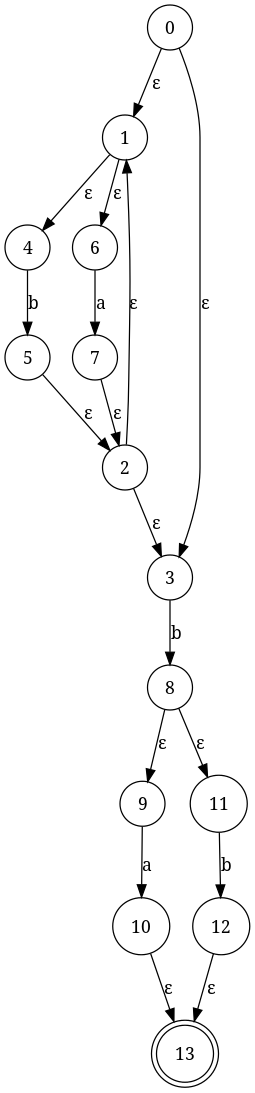
Тада! Э-э, я имею в виду, что и требовалось доказать.
хотите узнать больше?
все изображения выше были сгенерированы с помощью онлайн-инструмент для автоматического преобразования регулярных выражений в недетерминированные конечные автоматы. Вы можете найти его исходный код для Thompson-McNaughton-Yamada Алгоритм построения онлайн.
алгоритм также рассматривается в компиляторы Aho: принципы, методы и инструменты, хотя его объяснение скудно по деталям реализации. Вы также можете узнать из реализация конструкции Томпсона в C от превосходного Расса Кокса, который описал его некоторые детали в популярной статье о регулярные выражения.
в репозитории GitHub ниже вы можете найти Java-реализацию конструкции Томпсона, где сначала создается NFA из регулярного выражения, а затем сопоставляется входная строка с этим NFA:
