Silverlight поворот и масштабирование растрового изображения, чтобы вписаться в прямоугольник без обрезки
Мне нужно повернуть WriteableBitmap и масштабировать его вниз или вверх, прежде чем он будет обрезан.
мой текущий код будет вращаться, но будет обрезать края, если высота больше, чем ширина.
Я предполагаю, что мне нужно масштабировать?
public WriteableBitmap Rotate(WriteableBitmap Source, double Angle)
{
RotateTransform rt = new RotateTransform();
rt.Angle = Angle;
TransformGroup transform = new TransformGroup();
transform.Children.Add(rt);
Image tempImage2 = new Image();
WriteableBitmap wb;
rt.CenterX = Source.PixelWidth / 2;
rt.CenterY = Source.PixelHeight / 2;
tempImage2.Width = Source.PixelWidth;
tempImage2.Height = Source.PixelHeight;
wb = new WriteableBitmap((int)(Source.PixelWidth), Source.PixelHeight);
tempImage2.Source = Source;
tempImage2.UpdateLayout();
wb.Render(tempImage2, transform);
wb.Invalidate();
return wb;
}
Как уменьшить изображение, чтобы оно не было обрезано? Или есть другой способ?
1 ответов
вам нужно рассчитать масштабирование на основе вращения углов относительно центра.
Если изображение квадратное, нужен только один угол, но для прямоугольника вам нужно проверить 2 угла, чтобы увидеть, перекрывается ли вертикальный или горизонтальный край. Эта проверка представляет собой линейное сравнение превышения высоты и ширины прямоугольника.
Нажмите здесь для рабочего приложения testbed, созданного для этого ответа (изображение ниже):
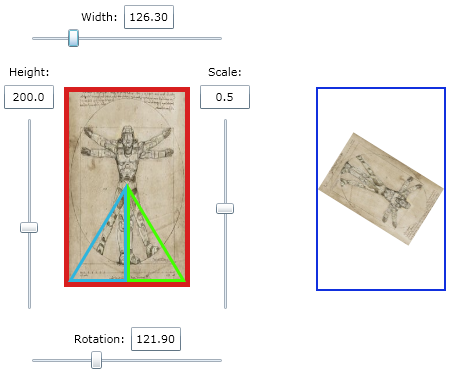
double CalculateConstraintScale(double rotation, int pixelWidth, int pixelHeight)
псевдо-код выглядит следующим образом (фактический код C# в конце):
- преобразовать угол поворота в радианы
- вычислить "радиус" от центра прямоугольника до угла
- преобразовать угловое положение BR в полярные координаты
- преобразовать угловое положение BL в полярные координаты
- применить вращение к обеим полярным координатам
- преобразовать новые позиции вернуться к декартовым координатам (значение ABS)
- найдите самое большое из 2 горизонтальных положений
- найдите самую большую из 2 вертикальных позиций
- рассчитать изменение дельты для горизонтального размера
- рассчитать изменение дельты для вертикального размере
- возвращенная ширина / 2 / x если горизонтальное изменение больше
- возвращенная высота / 2 / y если вертикальное изменение больше
результат множитель, который будет масштабировать изображение вниз, чтобы соответствовать исходному прямоугольнику независимо от вращения.
**Примечание: хотя можно сделать большую часть математики с использованием матричных операций, недостаточно вычислений, чтобы гарантировать это. Я также подумал, что это будет лучшим примером из первых принципов.*
C# Код:
/// <summary>
/// Calculate the scaling required to fit a rectangle into a rotation of that same rectangle
/// </summary>
/// <param name="rotation">Rotation in degrees</param>
/// <param name="pixelWidth">Width in pixels</param>
/// <param name="pixelHeight">Height in pixels</param>
/// <returns>A scaling value between 1 and 0</returns>
/// <remarks>Released to the public domain 2011 - David Johnston (HiTech Magic Ltd)</remarks>
private double CalculateConstraintScale(double rotation, int pixelWidth, int pixelHeight)
{
// Convert angle to radians for the math lib
double rotationRadians = rotation * PiDiv180;
// Centre is half the width and height
double width = pixelWidth / 2.0;
double height = pixelHeight / 2.0;
double radius = Math.Sqrt(width * width + height * height);
// Convert BR corner into polar coordinates
double angle = Math.Atan(height / width);
// Now create the matching BL corner in polar coordinates
double angle2 = Math.Atan(height / -width);
// Apply the rotation to the points
angle += rotationRadians;
angle2 += rotationRadians;
// Convert back to rectangular coordinate
double x = Math.Abs(radius * Math.Cos(angle));
double y = Math.Abs(radius * Math.Sin(angle));
double x2 = Math.Abs(radius * Math.Cos(angle2));
double y2 = Math.Abs(radius * Math.Sin(angle2));
// Find the largest extents in X & Y
x = Math.Max(x, x2);
y = Math.Max(y, y2);
// Find the largest change (pixel, not ratio)
double deltaX = x - width;
double deltaY = y - height;
// Return the ratio that will bring the largest change into the region
return (deltaX > deltaY) ? width / x : height / y;
}
пример использования:
private WriteableBitmap GenerateConstrainedBitmap(BitmapImage sourceImage, int pixelWidth, int pixelHeight, double rotation)
{
double scale = CalculateConstraintScale(rotation, pixelWidth, pixelHeight);
// Create a transform to render the image rotated and scaled
var transform = new TransformGroup();
var rt = new RotateTransform()
{
Angle = rotation,
CenterX = (pixelWidth / 2.0),
CenterY = (pixelHeight / 2.0)
};
transform.Children.Add(rt);
var st = new ScaleTransform()
{
ScaleX = scale,
ScaleY = scale,
CenterX = (pixelWidth / 2.0),
CenterY = (pixelHeight / 2.0)
};
transform.Children.Add(st);
// Resize to specified target size
var tempImage = new Image()
{
Stretch = Stretch.Fill,
Width = pixelWidth,
Height = pixelHeight,
Source = sourceImage,
};
tempImage.UpdateLayout();
// Render to a writeable bitmap
var writeableBitmap = new WriteableBitmap(pixelWidth, pixelHeight);
writeableBitmap.Render(tempImage, transform);
writeableBitmap.Invalidate();
return writeableBitmap;
}
