Случайное число из гистограммы
предположим, я создаю гистограмму с помощью scipy / numpy, поэтому у меня есть два массива: один для подсчета bin и один для ребер bin. Если я использую гистограмму для представления функции распределения вероятностей, как я могу эффективно генерировать случайные числа из этого распределения?
4 ответов
Это, наверное, то, что np.random.choice делает в ответе @Ophion, но вы можете построить нормализованную функцию кумулятивной плотности, а затем выбрать на основе равномерного случайного числа:
from __future__ import division
import numpy as np
import matplotlib.pyplot as plt
data = np.random.normal(size=1000)
hist, bins = np.histogram(data, bins=50)
bin_midpoints = bins[:-1] + np.diff(bins)/2
cdf = np.cumsum(hist)
cdf = cdf / cdf[-1]
values = np.random.rand(10000)
value_bins = np.searchsorted(cdf, values)
random_from_cdf = bin_midpoints[value_bins]
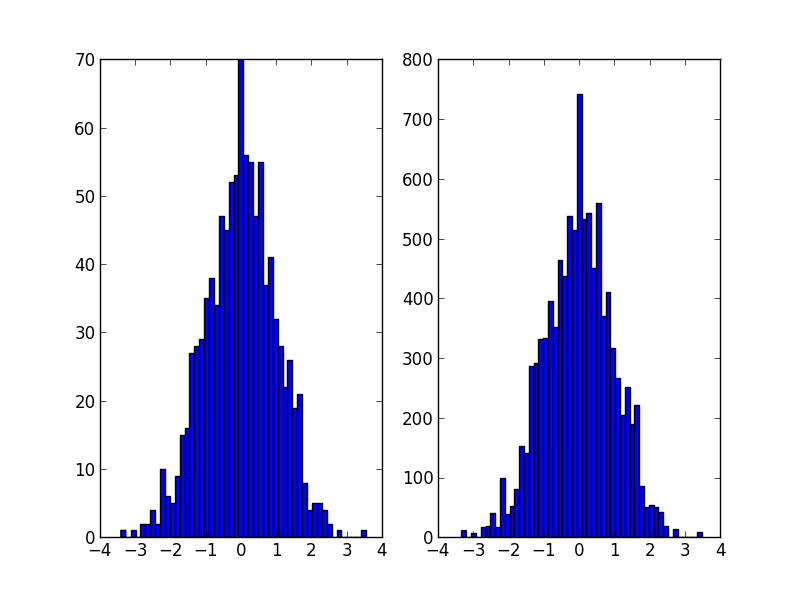
plt.subplot(121)
plt.hist(data, 50)
plt.subplot(122)
plt.hist(random_from_cdf, 50)
plt.show()
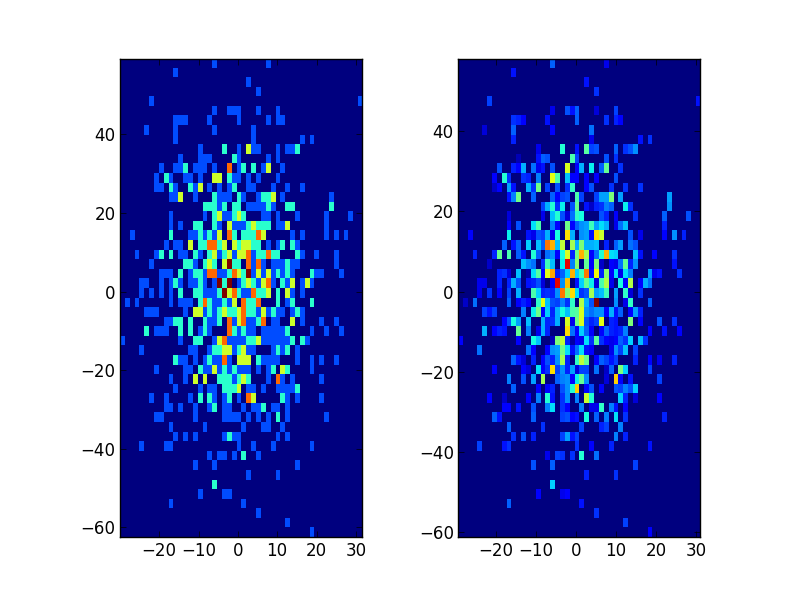
2D случай можно сделать следующим образом:
data = np.column_stack((np.random.normal(scale=10, size=1000),
np.random.normal(scale=20, size=1000)))
x, y = data.T
hist, x_bins, y_bins = np.histogram2d(x, y, bins=(50, 50))
x_bin_midpoints = x_bins[:-1] + np.diff(x_bins)/2
y_bin_midpoints = y_bins[:-1] + np.diff(y_bins)/2
cdf = np.cumsum(hist.ravel())
cdf = cdf / cdf[-1]
values = np.random.rand(10000)
value_bins = np.searchsorted(cdf, values)
x_idx, y_idx = np.unravel_index(value_bins,
(len(x_bin_midpoints),
len(y_bin_midpoints)))
random_from_cdf = np.column_stack((x_bin_midpoints[x_idx],
y_bin_midpoints[y_idx]))
new_x, new_y = random_from_cdf.T
plt.subplot(121, aspect='equal')
plt.hist2d(x, y, bins=(50, 50))
plt.subplot(122, aspect='equal')
plt.hist2d(new_x, new_y, bins=(50, 50))
plt.show()
@Jaime решение отлично, но вы должны рассмотреть возможность использования KDE (оценка плотности ядра) гистограммы. Отличное объяснение, почему проблематично делать статистику по гистограмме, и почему вы должны использовать kde вместо этого, можно найти здесь
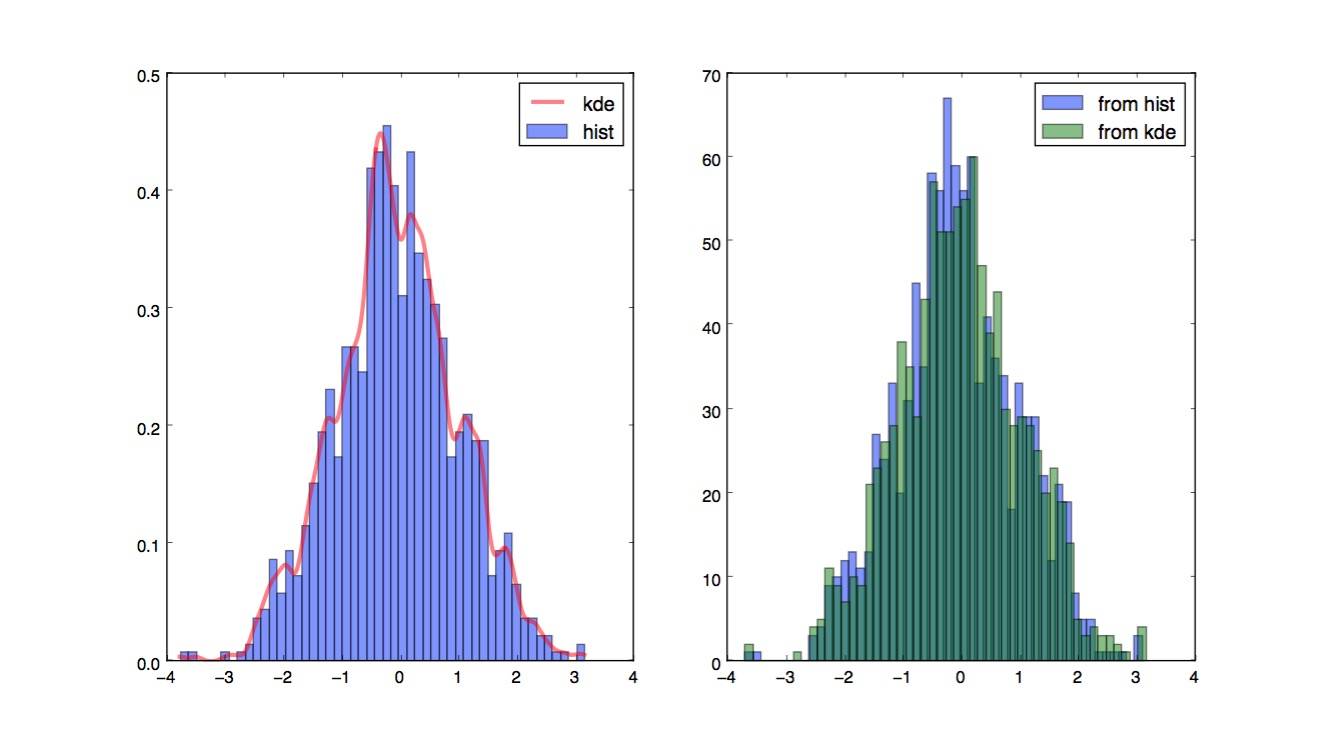
я отредактировал код @ Jaime, чтобы показать, как использовать kde из scipy. Он выглядит почти так же, но лучше захватывает генератор гистограмм.
from __future__ import division
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gaussian_kde
def run():
data = np.random.normal(size=1000)
hist, bins = np.histogram(data, bins=50)
x_grid = np.linspace(min(data), max(data), 1000)
kdepdf = kde(data, x_grid, bandwidth=0.1)
random_from_kde = generate_rand_from_pdf(kdepdf, x_grid)
bin_midpoints = bins[:-1] + np.diff(bins) / 2
random_from_cdf = generate_rand_from_pdf(hist, bin_midpoints)
plt.subplot(121)
plt.hist(data, 50, normed=True, alpha=0.5, label='hist')
plt.plot(x_grid, kdepdf, color='r', alpha=0.5, lw=3, label='kde')
plt.legend()
plt.subplot(122)
plt.hist(random_from_cdf, 50, alpha=0.5, label='from hist')
plt.hist(random_from_kde, 50, alpha=0.5, label='from kde')
plt.legend()
plt.show()
def kde(x, x_grid, bandwidth=0.2, **kwargs):
"""Kernel Density Estimation with Scipy"""
kde = gaussian_kde(x, bw_method=bandwidth / x.std(ddof=1), **kwargs)
return kde.evaluate(x_grid)
def generate_rand_from_pdf(pdf, x_grid):
cdf = np.cumsum(pdf)
cdf = cdf / cdf[-1]
values = np.random.rand(1000)
value_bins = np.searchsorted(cdf, values)
random_from_cdf = x_grid[value_bins]
return random_from_cdf
возможно, что-то вроде этого. Использует счетчик гистограммы в качестве веса и выбирает значения индексов на основе этого веса.
import numpy as np
initial=np.random.rand(1000)
values,indices=np.histogram(initial,bins=20)
values=values.astype(np.float32)
weights=values/np.sum(values)
#Below, 5 is the dimension of the returned array.
new_random=np.random.choice(indices[1:],5,p=weights)
print new_random
#[ 0.55141614 0.30226256 0.25243184 0.90023117 0.55141614]
у меня была та же проблема, что и OP, и я хотел бы поделиться своим подходом к этой проблеме.
после Хайме ответ и Ноам Пелед ответ Я построил решение для 2D-задачи, используя оценка плотности ядра (KDE).
Фрист, давайте генерировать некоторые случайные данные, а затем вычислить его функция плотности вероятности (PDF) из KDE. Я буду использовать пример доступен в SciPy для что.
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
def measure(n):
"Measurement model, return two coupled measurements."
m1 = np.random.normal(size=n)
m2 = np.random.normal(scale=0.5, size=n)
return m1+m2, m1-m2
m1, m2 = measure(2000)
xmin = m1.min()
xmax = m1.max()
ymin = m2.min()
ymax = m2.max()
X, Y = np.mgrid[xmin:xmax:100j, ymin:ymax:100j]
positions = np.vstack([X.ravel(), Y.ravel()])
values = np.vstack([m1, m2])
kernel = stats.gaussian_kde(values)
Z = np.reshape(kernel(positions).T, X.shape)
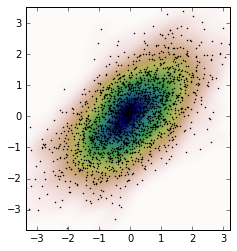
fig, ax = plt.subplots()
ax.imshow(np.rot90(Z), cmap=plt.cm.gist_earth_r,
extent=[xmin, xmax, ymin, ymax])
ax.plot(m1, m2, 'k.', markersize=2)
ax.set_xlim([xmin, xmax])
ax.set_ylim([ymin, ymax])
и земельный участок:
теперь мы получаем случайные данные из PDF, полученные из KDE, который является переменной Z.
# Generate the bins for each axis
x_bins = np.linspace(xmin, xmax, Z.shape[0]+1)
y_bins = np.linspace(ymin, ymax, Z.shape[1]+1)
# Find the middle point for each bin
x_bin_midpoints = x_bins[:-1] + np.diff(x_bins)/2
y_bin_midpoints = y_bins[:-1] + np.diff(y_bins)/2
# Calculate the Cumulative Distribution Function(CDF)from the PDF
cdf = np.cumsum(Z.ravel())
cdf = cdf / cdf[-1] # Normalização
# Create random data
values = np.random.rand(10000)
# Find the data position
value_bins = np.searchsorted(cdf, values)
x_idx, y_idx = np.unravel_index(value_bins,
(len(x_bin_midpoints),
len(y_bin_midpoints)))
# Create the new data
new_data = np.column_stack((x_bin_midpoints[x_idx],
y_bin_midpoints[y_idx]))
new_x, new_y = new_data.T
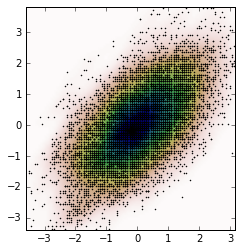
и мы можем вычислить KDE из этих новых данных и построить его.
kernel = stats.gaussian_kde(new_data.T)
new_Z = np.reshape(kernel(positions).T, X.shape)
fig, ax = plt.subplots()
ax.imshow(np.rot90(new_Z), cmap=plt.cm.gist_earth_r,
extent=[xmin, xmax, ymin, ymax])
ax.plot(new_x, new_y, 'k.', markersize=2)
ax.set_xlim([xmin, xmax])
ax.set_ylim([ymin, ymax])