Способы реализации поиска в глубину для графа с нерекурсивный подход
Ну, я потратил много времени на этот вопрос. Однако я могу найти решения только с нерекурсивными методами для дерева:не рекурсивный для дерева, или рекурсивный метод для графа, рекурсивный для graph.
и многие учебники (я не предоставляю эти ссылки здесь) также не предоставляют подходы. Или учебник совершенно неверен. Пожалуйста, помогите мне.
обновление:
Это действительно трудно опишите:
если у меня есть неориентированный граф:
1
/ |
4 | 2
3 /
1-- 2-- 3 --1 цикл.
на шаг: push the neighbors of the popped vertex into the stack
WHAT'S THE ORDER OF THE VERTEXES SHOULD BE PUSHED?
если выталкиваемый порядок равен 2 4 3, вершина в стеке:
| |
|3|
|4|
|2|
_
после извлечения узлов, мы получили результат: 1 -> 3 -> 4 -> 2 вместо 1--> 3 --> 2 -->4.
ЭТО НЕВЕРНО. КАКОЕ УСЛОВИЕ СЛЕДУЕТ ДОБАВИТЬ, ЧТОБЫ ОСТАНОВИТЬ ЭТОТ СЦЕНАРИЙ?
13 ответов
DFS без рекурсии в основном совпадает с BFS - но использовать стек вместо очереди в качестве структуры данных.
нить итеративный DFS vs рекурсивный DFS и различные элементы порядка ручки с обоими подходами и разница между ними (и есть! вы не будете пересекать узлы в том же порядке!)
алгоритм итерационного подхода в основном:
DFS(source):
s <- new stack
visited <- {} // empty set
s.push(source)
while (s is not empty):
current <- s.pop()
if (current is in visited):
continue
visited.add(current)
// do something with current
for each node v such that (current,v) is an edge:
s.push(v)
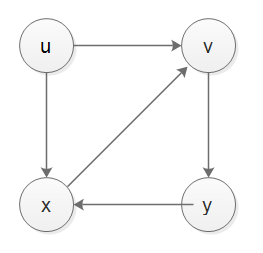
Это не ответ, а расширенный комментарий, показывающий применение алгоритма в ответе @amit на график в текущей версии вопроса, предполагая, что 1 является начальным узлом, а его соседи выталкиваются в порядке 2, 4, 3:
1
/ | \
4 | 2
3 /
Actions Stack Visited
======= ===== =======
push 1 [1] {}
pop and visit 1 [] {1}
push 2, 4, 3 [2, 4, 3] {1}
pop and visit 3 [2, 4] {1, 3}
push 1, 2 [2, 4, 1, 2] {1, 3}
pop and visit 2 [2, 4, 1] {1, 3, 2}
push 1, 3 [2, 4, 1, 1, 3] {1, 3, 2}
pop 3 (visited) [2, 4, 1, 1] {1, 3, 2}
pop 1 (visited) [2, 4, 1] {1, 3, 2}
pop 1 (visited) [2, 4] {1, 3, 2}
pop and visit 4 [2] {1, 3, 2, 4}
push 1 [2, 1] {1, 3, 2, 4}
pop 1 (visited) [2] {1, 3, 2, 4}
pop 2 (visited) [] {1, 3, 2, 4}
таким образом, применение алгоритма, толкающего соседей 1 в порядке 2, 4, 3, приводит к порядку посещения 1, 3, 2, 4. Независимо от порядка push для соседей 1, 2 и 3 будут смежными в порядке посещения, потому что в зависимости от того, посещенный первый будет толкать другой, который еще не посетил, а также 1, который был посещен.
логика DFS должна быть:
1) если текущий узел не посещается, посетите узел и отметьте его как посещенный
2) для всех своих соседей, которые не были посещены, нажмите их в стек
например, давайте определим класс GraphNode в Java:
class GraphNode {
int index;
ArrayList<GraphNode> neighbors;
}
и вот DFS без рекурсии:
void dfs(GraphNode node) {
// sanity check
if (node == null) {
return;
}
// use a hash set to mark visited nodes
Set<GraphNode> set = new HashSet<GraphNode>();
// use a stack to help depth-first traversal
Stack<GraphNode> stack = new Stack<GraphNode>();
stack.push(node);
while (!stack.isEmpty()) {
GraphNode curr = stack.pop();
// current node has not been visited yet
if (!set.contains(curr)) {
// visit the node
// ...
// mark it as visited
set.add(curr);
}
for (int i = 0; i < curr.neighbors.size(); i++) {
GraphNode neighbor = curr.neighbors.get(i);
// this neighbor has not been visited yet
if (!set.contains(neighbor)) {
stack.push(neighbor);
}
}
}
}
мы можем использовать ту же логику для рекурсивного выполнения DFS, клонирования графа и т. д.
Рекурсия-это способ использования стека вызовов для хранения состояния обхода графика. Вы можете использовать стек явно, скажем, имея локальную переменную типа std::stack, тогда вам не понадобится рекурсия для реализации DFS, а просто цикл.
ОК. если вы все еще ищете код java
dfs(Vertex start){
Stack<Vertex> stack = new Stack<>(); // initialize a stack
List<Vertex> visited = new ArrayList<>();//maintains order of visited nodes
stack.push(start); // push the start
while(!stack.isEmpty()){ //check if stack is empty
Vertex popped = stack.pop(); // pop the top of the stack
if(!visited.contains(popped)){ //backtrack if the vertex is already visited
visited.add(popped); //mark it as visited as it is not yet visited
for(Vertex adjacent: popped.getAdjacents()){ //get the adjacents of the vertex as add them to the stack
stack.add(adjacent);
}
}
}
for(Vertex v1 : visited){
System.out.println(v1.getId());
}
}
Python-кода. Сложность времени O(V+E), где V и E - количество вершин и ребер соответственно. Сложность пространства равна O (V) из-за наихудшего случая, когда есть путь, содержащий каждую вершину без какого-либо обратного отслеживания (т. е. путь поиска является линейные цепи).
в стеке хранятся кортежи формы (vertex, vertex_edge_index), так что DFS может быть возобновлен из определенной вершины на краю сразу после последнего края, который был обработан из этой вершины (так же, как стек вызовов функций рекурсивного DFS).
в примере кода используется полный диграф где каждая вершина связана с каждой другой вершиной. Следовательно, нет необходимости хранить явный список ребер для каждого узла, так как граф является списком ребер (graph G содержит все вершина.)
numv = 1000
print('vertices =', numv)
G = [Vertex(i) for i in range(numv)]
def dfs(source):
s = []
visited = set()
s.append((source,None))
time = 1
space = 0
while s:
time += 1
current, index = s.pop()
if index is None:
visited.add(current)
index = 0
# vertex has all edges possible: G is a complete graph
while index < len(G) and G[index] in visited:
index += 1
if index < len(G):
s.append((current,index+1))
s.append((G[index], None))
space = max(space, len(s))
print('time =', time, '\nspace =', space)
dfs(G[0])
выход:
time = 2000
space = 1000
отметим, что времени вот измерения V операции, а не E. Значение numv*2, потому что каждая вершина рассматривается дважды, один раз при открытии и один раз при завершении.
вообще-стек не в состоянии справиться с обнаружить время и время окончания, если мы хотим реализовать DFS со стеком, и хотят иметь дело с знакомства и времени, нам придется прибегнуть к другой рекордер стека, моя реализация будет показано ниже, имеют тест правильный, ниже корпус-1, корпус-2 и 3 графа.
from collections import defaultdict
class Graph(object):
adj_list = defaultdict(list)
def __init__(self, V):
self.V = V
def add_edge(self,u,v):
self.adj_list[u].append(v)
def DFS(self):
visited = []
instack = []
disc = []
fini = []
for t in range(self.V):
visited.append(0)
disc.append(0)
fini.append(0)
instack.append(0)
time = 0
for u_ in range(self.V):
if (visited[u_] != 1):
stack = []
stack_recorder = []
stack.append(u_)
while stack:
u = stack.pop()
visited[u] = 1
time+=1
disc[u] = time
print(u)
stack_recorder.append(u)
flag = 0
for v in self.adj_list[u]:
if (visited[v] != 1):
flag = 1
if instack[v]==0:
stack.append(v)
instack[v]= 1
if flag == 0:
time+=1
temp = stack_recorder.pop()
fini[temp] = time
while stack_recorder:
temp = stack_recorder.pop()
time+=1
fini[temp] = time
print(disc)
print(fini)
if __name__ == '__main__':
V = 6
G = Graph(V)
#==============================================================================
# #for case 1
# G.add_edge(0,1)
# G.add_edge(0,2)
# G.add_edge(1,3)
# G.add_edge(2,1)
# G.add_edge(3,2)
#==============================================================================
#==============================================================================
# #for case 2
# G.add_edge(0,1)
# G.add_edge(0,2)
# G.add_edge(1,3)
# G.add_edge(3,2)
#==============================================================================
#for case 3
G.add_edge(0,3)
G.add_edge(0,1)
G.add_edge(1,4)
G.add_edge(2,4)
G.add_edge(2,5)
G.add_edge(3,1)
G.add_edge(4,3)
G.add_edge(5,5)
G.DFS()
Я думаю, вам нужно использовать visited[n] логический массив, чтобы проверить, посещается ли текущий узел или нет ранее.
рекурсивный алгоритм работает очень хорошо для DFS, поскольку мы пытаемся погрузиться как можно глубже, т. е. как только мы найдем неисследованную вершину, мы сразу же исследуем ее первого неисследованного соседа. Вам нужно вырваться из цикла for, как только вы найдете первого неисследованного соседа.
for each neighbor w of v
if w is not explored
mark w as explored
push w onto the stack
BREAK out of the for loop
Я думаю, что это оптимизированный DFS в отношении пространства-исправьте меня, если я ошибаюсь.
s = stack
s.push(initial node)
add initial node to visited
while s is not empty:
v = s.peek()
if for all E(v,u) there is one unvisited u:
mark u as visited
s.push(u)
else
s.pop
использование стека и реализация, как это сделано стеком вызовов в процессе рекурсии -
идея состоит в том, чтобы подтолкнуть вершину в стеке, а затем подтолкнуть ее вершину, смежную с ней, которая хранится в списке смежности по индексу вершины, а затем продолжить этот процесс, пока мы не сможем двигаться дальше в графике, теперь, если мы не сможем двигаться вперед в графике, мы удалим вершину, которая в настоящее время находится на вершине стека, поскольку она не может взять нас на вершина непосещенных.
теперь, используя стек, мы заботимся о том, что вершина удаляется из стека только тогда, когда все вершины, которые могут быть исследованы из текущей вершины, были посещены, что было сделано процессом рекурсии автоматически.
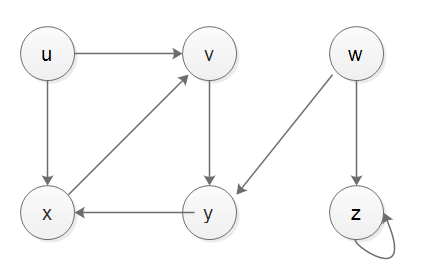
( 0 ( 1 ( 2 ( 4 4 ) 2 ) ( 3 3 ) 1 ) 0 ) ( 6 ( 5 5 ) ( 7 7 ) 6 )
в выше скобки показывают порядок, в котором вершина добавляется в стек и удаляется из стека, поэтому скобка для вершины закрывается только тогда, когда все вершины, которые можно посетить из нее, были сделаны.
(здесь я использовал представление списка смежности и реализован как вектор списка (вектор > AdjList) с помощью C++ STL)
void DFSUsingStack() {
/// we keep a check of the vertices visited, the vector is set to false for all vertices initially.
vector<bool> visited(AdjList.size(), false);
stack<int> st;
for(int i=0 ; i<AdjList.size() ; i++){
if(visited[i] == true){
continue;
}
st.push(i);
cout << i << '\n';
visited[i] = true;
while(!st.empty()){
int curr = st.top();
for(list<int> :: iterator it = AdjList[curr].begin() ; it != AdjList[curr].end() ; it++){
if(visited[*it] == false){
st.push(*it);
cout << (*it) << '\n';
visited[*it] = true;
break;
}
}
/// We can move ahead from current only if a new vertex has been added on the top of the stack.
if(st.top() != curr){
continue;
}
st.pop();
}
}
}
следующий код Java будет удобен: -
private void DFS(int v,boolean[] visited){
visited[v]=true;
Stack<Integer> S = new Stack<Integer>();
S.push(v);
while(!S.isEmpty()){
int v1=S.pop();
System.out.println(adjLists.get(v1).name);
for(Neighbor nbr=adjLists.get(v1).adjList; nbr != null; nbr=nbr.next){
if (!visited[nbr.VertexNum]){
visited[nbr.VertexNum]=true;
S.push(nbr.VertexNum);
}
}
}
}
public void dfs() {
boolean[] visited = new boolean[adjLists.size()];
for (int v=0; v < visited.length; v++) {
if (!visited[v])/*This condition is for Unconnected Vertices*/ {
System.out.println("\nSTARTING AT " + adjLists.get(v).name);
DFS(v, visited);
}
}
}
многие люди скажут, что нерекурсивный DFS-это просто BFS со стеком, а не с очередью. Это не точно, позвольте мне объяснить немного больше.
рекурсивный DFS
рекурсивный DFS использует стек вызовов для сохранения состояния, то есть вы не управляете отдельным стеком самостоятельно.
однако для большого графика рекурсивная DFS (или любая рекурсивная функция) может привести к глубокой рекурсии, которая может привести к сбою вашей проблемы с переполнением стека (не этот сайт, реальная вещь).
нерекурсивный DFS
DFS не то же самое, что BFS. Он имеет другое использование пространства, но если вы реализуете его так же, как BFS, но используя стек, а не очередь, вы будете использовать больше места, чем нерекурсивные DFS.
почему больше пространства?
рассмотрим следующий пример:
// From non-recursive "DFS"
for (auto i&: adjacent) {
if (!visited(i)) {
stack.push(i);
}
}
и сравните это с этим:
// From recursive DFS
for (auto i&: adjacent) {
if (!visited(i)) {
dfs(i);
}
}
в первом фрагменте кода Вы помещаете все соседние узлы в стек перед итерацией к следующей смежной вершине, и это имеет стоимость пространства. Если график большой, это может иметь существенное значение.
Что делать тогда?
Если вы решите решить проблему пространства, повторяя список смежности снова после появления стека, это добавит стоимость сложности времени.
одним из решений является добавление элементов в стек один за другим, как вы посетите их. Для этого вы можете сохранить итератор в стеке, чтобы возобновить итерации после выталкивания.
ленивый способ
В C/C++ ленивый подход заключается в компиляции вашей программы с большим размером стека и увеличении размера стека через ulimit, но это действительно паршиво. В Java вы можете установить размер стека в качестве параметра JVM.