среде MATLAB/Октава - обобщенное матричное умножение

вот немного более полированная версия решения, которое вы опубликовали, с некоторыми небольшими улучшениями.

мы проверяем, есть ли у нас больше строк, чем столбцов или наоборот, а затем делаем умножение соответственно, выбирая либо умножать строки с матрицами, либо матрицы со столбцами (таким образом, делая наименьшее количество итераций цикла).

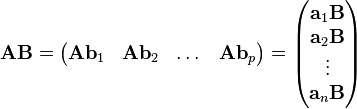
Примечание: это не всегда может быть лучшей стратегией (идет мимо строки вместо столбцов), даже если строк меньше, чем столбцов; тот факт, что массивы MATLAB хранятся в колонка-главный заказ в памяти делает его более эффективным для того чтобы отрезать столбцами, по мере того как элементы хранятся последовательно. В то время как доступ к строкам включает в себя обход элементов по успехов (что не является дружественным к кэшу -- think пространственная локальность).

кроме этого, код должен обрабатывать двойной/один/комплекс, полный / разреженный (и ошибки, где это не является возможной комбинацией). Он также уважает пустые матрицы и нулевые измерения.

function C = my_mtimes(A, B, outFcn, inFcn)
    % default arguments
    if nargin < 4, inFcn = @times; end
    if nargin < 3, outFcn = @sum; end

    % check valid input
    assert(ismatrix(A) && ismatrix(B), 'Inputs must be 2D matrices.');
    assert(isequal(size(A,2),size(B,1)),'Inner matrix dimensions must agree.');
    assert(isa(inFcn,'function_handle') && isa(outFcn,'function_handle'), ...
        'Expecting function handles.')

    % preallocate output matrix
    M = size(A,1);
    N = size(B,2);
    if issparse(A)
        args = {'like',A};
    elseif issparse(B)
        args = {'like',B};
    else
        args = {superiorfloat(A,B)};
    end
    C = zeros(M,N, args{:});

    % compute matrix multiplication
    % http://en.wikipedia.org/wiki/Matrix_multiplication#Inner_product
    if M < N
        % concatenation of products of row vectors with matrices
        % A*B = [a_1*B ; a_2*B ; ... ; a_m*B]
        for m=1:M
            %C(m,:) = A(m,:) * B;
            %C(m,:) = sum(bsxfun(@times, A(m,:)', B), 1);
            C(m,:) = outFcn(bsxfun(inFcn, A(m,:)', B), 1);
        end
    else
        % concatenation of products of matrices with column vectors
        % A*B = [A*b_1 , A*b_2 , ... , A*b_n]
        for n=1:N
            %C(:,n) = A * B(:,n);
            %C(:,n) = sum(bsxfun(@times, A, B(:,n)'), 2);
            C(:,n) = outFcn(bsxfun(inFcn, A, B(:,n)'), 2);
        end
    end
end

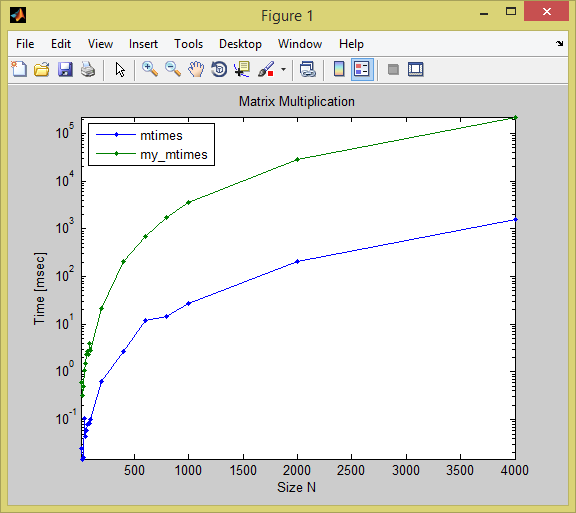
сравнение

функция, несомненно, медленнее во всем, но для больших размеров она на порядок хуже, чем встроенная матрица-умножение:

        (tic/toc times in seconds)
      (tested in R2014a on Windows 8)

    size      mtimes       my_mtimes 
    ____    __________     _________
     400     0.0026398       0.20282
     600      0.012039       0.68471
     800      0.014571        1.6922
    1000      0.026645        3.5107
    2000       0.20204         28.76
    4000        1.5578        221.51

вот тестовый код:

sz = [10:10:100 200:200:1000 2000 4000];
t = zeros(numel(sz),2);
for i=1:numel(sz)
    n = sz(i); disp(n)
    A = rand(n,n);
    B = rand(n,n);

    tic
    C = A*B;
    t(i,1) = toc;
    tic
    D = my_mtimes(A,B);
    t(i,2) = toc;

    assert(norm(C-D) < 1e-6)
    clear A B C D
end

semilogy(sz, t*1000, '.-')
legend({'mtimes','my_mtimes'}, 'Interpreter','none', 'Location','NorthWest')
xlabel('Size N'), ylabel('Time [msec]'), title('Matrix Multiplication')
axis tight

дополнительно

для полноты картины ниже приведены еще два наивных способы реализации обобщенного умножения матрицы (если вы хотите сравнить производительность, замените последнюю часть my_mtimes функция с любым из этих). Я даже не буду утруждать себя публикацией их прошедшего времени:)

C = zeros(M,N, args{:});
for m=1:M
    for n=1:N
        %C(m,n) = A(m,:) * B(:,n);
        %C(m,n) = sum(bsxfun(@times, A(m,:)', B(:,n)));
        C(m,n) = outFcn(bsxfun(inFcn, A(m,:)', B(:,n)));
    end
end

и другой способ (с тройным контуром):

C = zeros(M,N, args{:});
P = size(A,2); % = size(B,1);
for m=1:M
    for n=1:N
        for p=1:P
            %C(m,n) = C(m,n) + A(m,p)*B(p,n);
            %C(m,n) = plus(C(m,n), times(A(m,p),B(p,n)));
            C(m,n) = outFcn([C(m,n) inFcn(A(m,p),B(p,n))]);
        end
    end
end

что попробовать дальше?

если вы хотите выжать больше производительности, вам придется перейти на C / C++ MEX-файл, чтобы сократить накладные расходы интерпретируемого Код MATLAB. Вы все еще можете воспользоваться оптимизированными процедурами BLAS/LAPACK, вызвав их из MEX-файлов (см. вторая часть этого поста для примера). MATLAB поставляется с Intel MKL библиотека, которую, честно говоря, вы не можете победить, когда дело доходит до вычислений линейной алгебры на процессорах Intel.

другие уже упоминали несколько представлений об обмене файлами, которые реализуют универсальные матричные процедуры как MEX-файлы (см. @natan'ы ответ). Они особенно эффективны, если вы связываете их с оптимизированной библиотекой BLAS.