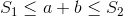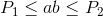Сумма и произведение в заданном диапазоне
даны четыре целых положительных числа 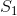 ,
, 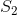 ,
, 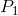 и
и 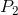 , есть ли способ быстро найти любые два числа
, есть ли способ быстро найти любые два числа  и
и 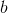 такое, что:
такое, что:
, когда 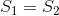 и
и 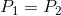 , существует закрытая форма
, существует закрытая форма 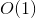 решение с помощью квадратных уравнений. Мы просто должны найти корни
решение с помощью квадратных уравнений. Мы просто должны найти корни 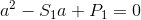 и это даст нам подходит
и это даст нам подходит  .
.
, когда 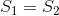 , Я знаю, как решить ее в
, Я знаю, как решить ее в 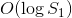 заметив, что кривая
заметив, что кривая 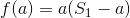 выпуклая и поэтому мы можем просто двоичный поиск подходящего
выпуклая и поэтому мы можем просто двоичный поиск подходящего  .
.
, когда 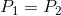 , это может быть решено в
, это может быть решено в 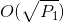 по факторингу
по факторингу 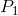 и ищет пару факторов, которые суммируются со значением в пределах диапазона.
и ищет пару факторов, которые суммируются со значением в пределах диапазона.
когда оба они являются диапазонами, однако, я не могу придумать какой-либо алгоритм, который может решить это эффективно. Существуют некоторые возможные эвристики, такие как фиксация одного из двух (итерация через меньший диапазон и т. д.), или немедленно сообщить, что нет пары, когда максимально возможное произведение, которое может быть сделано с суммированием двух целых чисел к 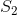 меньше, чем
меньше, чем 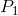 , etc.
, etc.
к сожалению, я не смог придумать ничего, что работало бы в общем случае быстрее, чем итерация через все в любом 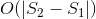 или
или 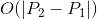 (возможно, с некоторыми дополнительными мелких факторов). Есть ли хороший алгоритм или какая-то причудливая математика, которая дает более быстрое решение?
(возможно, с некоторыми дополнительными мелких факторов). Есть ли хороший алгоритм или какая-то причудливая математика, которая дает более быстрое решение?
альтернативно, есть ли способ доказать, что итерация завершается быстро? (После обработки некоторых угловых случаев и т. д.) Меня не интересует количество допустимых пар; поиск любой пары будет делать. Похоже, что итерация по произведению и попытка найти соответствующую сумму имеют тенденцию быстро находить решение, если диапазон допустимых сумм достаточно велик. Могут ли быть какие-то доказательства?
Я был бы очень признателен за любую помощь!
1 ответов
вы можете решить его в O (sqrt (P2)) время.
найдите эти суммы: small_sum = I + ceiling(P1/i) и big_sum = i + floor(P2/i) для i между 1 и sqrt (P2).
Если small_sum > big_sum или big_sum С2, то я не партн решения. Двигаться дальше.
в противном случае max(small_sum, s1) min(big_sum, s2) и все значения между "хорошими суммами."Для любого из них пусть j = good_sum-i. Тогда i + j является a значение между s1 и s2, а i * j-между p1 и p2.
мы проверяем не более sqrt (P2) значений i, и для каждого из этих значений мы выполняем постоянную работу.
Edit -- Ruby реализация
def solve(s1, s2, p1, p2)
max_i = (p2**0.5).floor
1.upto(max_i) do |i|
small_sum = i + (p1/i.to_f).ceil
big_sum = i + (p2/i.to_f).floor
next if big_sum < s1 || small_sum > s2 || big_sum < small_sum
good_sum = [small_sum, s1].max
puts "sum: #{i} + #{good_sum - i} = #{good_sum}, #{s1} <= #{good_sum} <= #{s2}"
puts "product: #{i} * #{good_sum-i} = #{i*(good_sum-i)}, #{p1} <= #{i*(good_sum-i)} <= #{p2}"
return
end
puts "no solution"
end