Угол X между двумя 3D векторами?
У меня есть два 3D-вектора, называемые A и B, которые имеют только 3D-позицию. Я знаю, как найти угол вдоль единичной окружности в диапазоне от 0-360 градусов с помощью функции atan2 делать:
EDIT: (моя функция atan2 не имела смысла, теперь она должна найти "угол y" между 2 векторами):
toDegrees(atan2(A.x-B.x,A.z-B.z))+180
но это дает мне угол Y между 2 векторами. Мне нужно найти угол X между ними. Это связано с использованием значений позиций x, y и Z. Не x и z только, потому что это дает угол y между двумя векторами. Мне нужен угол X, я знаю, это звучит неопределенно, но я не знаю, как объяснить. Возможно, например, у вас есть камера в 3D-пространстве, если вы смотрите вверх или вниз, чем вращаете ось x. Но теперь мне нужно получить угол "вверх / вниз" между 2 векторами. Если я поверну эту 3D-камеру вдоль оси y, ось x не изменится. Таким образом, с 2 векторами, независимо от того, какой "угол y" находится между ними, угол x между 2 векторами останется неизменным, если угол y изменяется, потому что это угол" вверх/вниз", как в Камаре.
пожалуйста, помогите? Мне просто нужна строка math / pseudocode или объяснение. :)
3 ответов
вычисление угла высоты
хорошо, возможно, я наконец понял ваш комментарий ниже о том, что результат не зависит от y угол, и о том, как он относится к двум направлениям. Кажется, вы не очень заинтересованы в два векторы и угол между эти два, но вместо этого вы заинтересованы в разность векторов и угол, который образуется против горизонтальной плоскости. В горизонтальная система координат (часто используется в астрономии), этот угол будет называться "высота" или "высота", в отличие от "Азимута", который вы вычисляете с помощью формулы в вашем (отредактированном) вопросе. "высота" тесно связана с "угол наклона" вашей камеры, тогда как "Азимут" относится к "сдвиг".
у нас все еще есть проблема 2D. Одной из координат 2D-вектора является y координата разности векторов. Другой координат длина вектора после проецирования на горизонтальную плоскость, т. е. sqrt(x*x + z*z). Окончательное решение будет
x = A.x - B.x
y = A.y - B.y
z = A.z - B.z
alt = toDegrees(atan2(y, sqrt(x*x + z*z)))
az = toDegrees(atan2(-x, -z))
порядок (A - B В противоположность B - A) был выбран таким образом, что "A выше B" дает положительный y и поэтому положительная высота, в соответствии с вашим комментарием ниже. Знаки минус в вычислении Азимута выше должны заменить + 180 в коде из вашего вопроса, за исключением того, что диапазон сейчас [-180, 180] вместо ваш [0, 360]. Просто чтобы дать вам альтернативу, выберите то, что вы предпочитаете. Фактически вы вычисляете Азимут B - A в любом случае. Тот факт, что вы используете другой порядок для этих двух углов, может быть несколько запутанным, поэтому подумайте, действительно ли это то, что вы хотите, или вы хотите изменить знак высоты или изменить Азимут на 180°.
ортогональные проекции
для справки, я включу мой первоначальный ответ ниже, для тех, кто на самом деле ищет угол поворота вокруг некоторой фиксированной оси x, способ, предложенный в исходном вопросе.
если это X угол вы упоминаете в своем вопросе действительно угол поворота вокруг x axis, как показывает пример камеры, тогда вы можете подумать об этом следующим образом: установите x координата до нуля, и вы получите 2D-векторы в y-z самолет. Вы можете подумайте об этом как об ортогональной проекции на указанную равнину. Теперь вы вернулись к 2D-проблеме и можете решить ее там.
лично я бы просто позвонил atan2 дважды, один раз для каждого вектора, и вычесть получившиеся углы:
toDegrees(atan2(A.z, A.y) - atan2(B.z, B.y))
на x=0 подразумевается в приведенной выше формуле просто потому, что я работаю только на y и z.
я не совсем понял логику вашего сингла atan2 позвоните пока, но то, что я должен думать это говорит о том, что я не хотел бы поддерживать его, по крайней мере, без хорошего объяснительного комментария.
надеюсь, я правильно понял ваш вопрос, и это то, что вы ищете.
atan2(crossproduct.length,scalarproduct)
причиной использования atan2 вместо arccos или arcsin является точность. arccos ведет себя очень плохо вблизи 0 градусов. Небольшие ошибки вычисления в аргументе приведут к непропорционально большим ошибкам в результате. у arcsin такая же проблема близка к 90 градусам.
Так же, как 2D-векторы, вы вычисляете их угол, решая cos их Скалярное Произведение
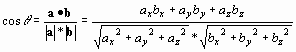
Вам не нужно Атан, вы всегда идете на точечный продукт, так как его фундаментальная операция векторов, а затем используете acos чтобы получить угол.
double angleInDegrees = acos ( cos(theta) ) * 180.0 / PI;
