Вычисление размера возможностей UID

в спецификации DICOM, UID определяется:9.1 ЮИД правила кодирования. Другими словами, действительны следующие идентификаторы DICOM UIDs:

  • "1.2.3.4.5"
  • "1.3.6.1.4.35045.103501438824148998807202626810206788999"
  • "1.2.826.0.1.3680043.2.1143.5028470438645158236649541857909059554"

при следующих незаконны Дицом UIDs:

  • ".1.2.3.4.5"
  • "1..2.3.4.5"
  • "1.2.3.4.5."
  • "1.2.3.4.05"
  • "12345"
  • "1.2.826.0.1.3680043.2.1143.50284704386451582366495418579090595540"

поэтому я знаю, что строка не более 64 байт и должна соответствовать следующему регулярному выражению [0-9.]+. Однако это регулярное выражение действительно суперсет, так как их намного меньше, чем (10+1)^64 (=4457915684525902395869512133369841539490161434991526715513934826241L) возможностей.

как бы точно вычисляется количество возможностей соблюдать правила DICOM UID ?

чтение правила корня / суффикса организации ясно указывает на то, что мне нужна хотя бы одна точка ('.'). В этом случае комбинация составляет не менее 3 байт (char) в виде: [0-9].[0-9]. В этом случае есть 10x10=100 возможности для UID длины 3.

глядя на первый ответ, кажется, что-то неясное о:

первая цифра каждого компонент не должен быть равен нулю, если компонент представляет собой одну цифру.

это значит, что:

  • "0.0" является действительным
  • "00.0" или "1.01" являются недопустимыми

таким образом, я бы сказал, что правильным выражением было бы:

(([1-9][0-9]*)|0)(.([1-9][0-9]*|0))+

используя простой код C, я мог бы найти:

  • f (0) = 0
  • f (1) = 0
  • f (2) = 0
  • f (3) = 100
  • f (4) = 1800
  • f (5) = 27100
  • f (6) = 369000
  • f (7) = 4753000
  • f (8) = 59049000

проверка корневой части UID выходит за рамки этого вопроса. Второй шаг проверки может позаботиться об отклонении некоторого OID, который невозможно зарегистрировать (некоторые люди упоминают ограничение на первую и вторую дугу, например). Для простоты мы примем все возможные (допустимые) корневые UID.

16
dicom math uid

2 ответов

в то время как мой другой ответ хорошо заботится об этом конкретном приложении, вот более общий подход. Он заботится о ситуациях, когда у вас есть другое регулярное выражение, описывающее рассматриваемый язык. Он также позволяет значительно увеличить длину строки, так как для этого требуется только O (log n) арифметические операции для вычисления количества комбинаций для строк длиной до n. В этом случае количество строк растет так быстро, что стоимость из этих арифметических операций резко вырастет, но это может быть не так для других, в противном случае подобных ситуаций.

построить конечный автомат

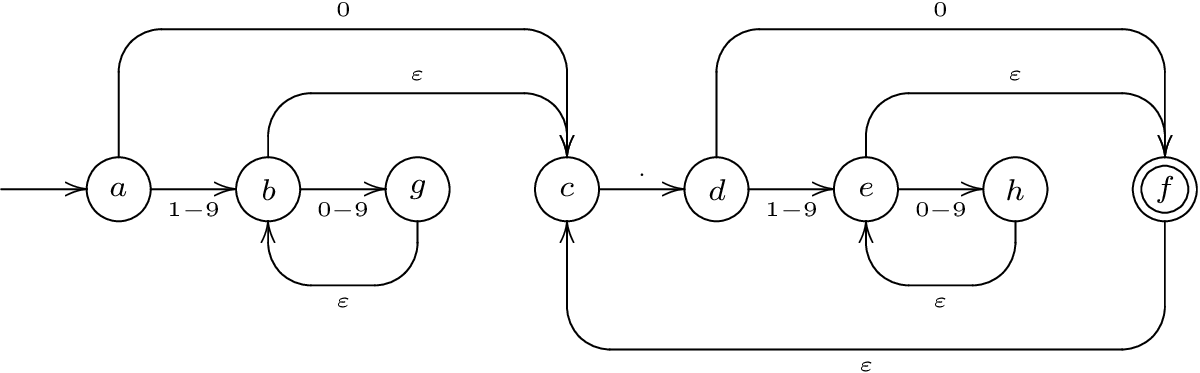
начать с обычный описание выражения вашего языка. Перевести регулярное выражение в конечный автомат. В вашем случае регулярное выражение может быть задано как

(([1-9][0-9]*)|0)(\.([1-9][0-9]*|0))+

автомат может выглядеть как это:

Finite State Automaton corresponding to regular expression

исключить ε-переходы

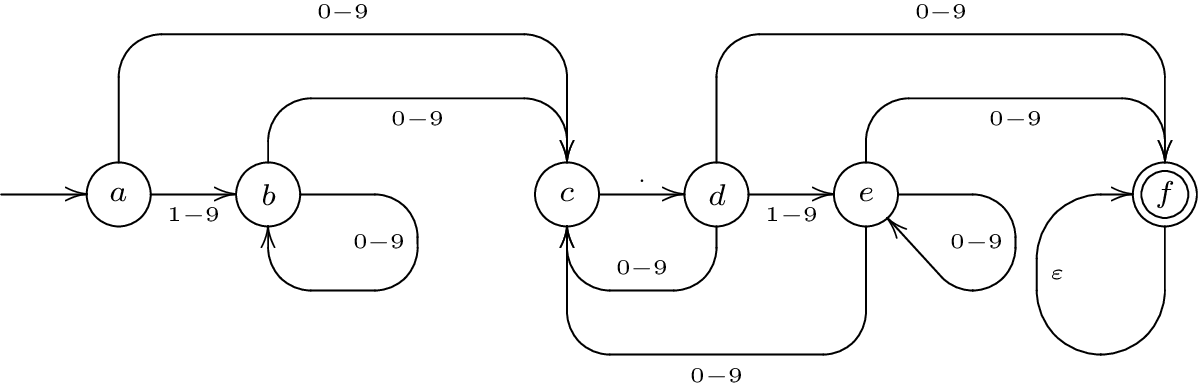
этот автомат обычно содержит ε-переходы (т. е. переходы состояний, которые не соответствуют никакому входному символу). Удалите их, чтобы один переход соответствовал одному символу ввода. Затем добавьте ε-переход в принимающее состояние(состояния). Если принимающие состояния имеют другие исходящие переходы, не добавляйте к ним ε-петли, а вместо этого добавьте ε-переход в принимающее состояние без исходящих ребер, а затем добавьте цикл к этому. Это можно рассматривать как заполнение входа ε на его конце, не допуская ε в середине. Взятые вместе, это преобразование гарантирует, что выполнение точно n переходы состояния соответствуют обработке ввода n символов или меньше. Модифицированный автомат может выглядеть так:

Finite State Automaton after changes to epsilon transitions

обратите внимание, что оба конструкция первого автомата из регулярного выражения и устранение ε-переходов может выполняться автоматически (и, возможно, даже в один шаг. Полученные автоматы могут быть более сложными, чем то, что я построил здесь вручную, но принцип тот же.

обеспечение уникальных путей

вам не нужно делать автомат детерминированные в том смысле, что для каждой комбинации исходного состояния и входного символа есть только одно целевое состояние. Это не так в моем вручную построенном. Но вы должны убедиться, что каждый полный ввод имеет только один возможный путь к принимающему состоянию, так как вы по существу будете считать пути. делает автомат детерминированным также обеспечит это более слабое свойство, поэтому перейдите к этому, если вы не можете обеспечить уникальные пути без этого. В моем примере длина каждого компонента четко определяет, какой путь использовать, поэтому я не сделал этого детерминированный. Но я включил пример с детерминированным подходом в конце этого поста.

построить матрицу перехода

Далее запишите матрицу перехода. Свяжите строки и столбцы с вашими состояниями (в порядке a, b, c, d, e, f в моем примере). Для каждой стрелки в автомате запишите количество символов, включенных в метку этой стрелки в столбце, связанном с исходным состоянием, и строке, связанной с целевым состоянием этой стрелы.

⎛ 0  0  0  0  0  0⎞
⎜ 9 10  0  0  0  0⎟
⎜10 10  0 10 10  0⎟
⎜ 0  0  1  0  0  0⎟
⎜ 0  0  0  9 10  0⎟
⎝ 0  0  0 10 10  1⎠

считайте результат с этой матрицы

теперь применение этой матрицы с вектором столбца один раз имеет следующее значение: если количество возможных способов прибытия в заданное состояние закодировано во входном векторе, выходной вектор дает вам количество способов одного перехода позже. Возьмите 64-ю степень этой матрицы, сконцентрируйтесь на первом столбце (так как Ste start ситуация кодируется как (1,0,0,0,0,0), что означает только один способ закончить в начале state) и суммировать все записи, соответствующие принимающим состояниям (только последний в этом случае). Нижний левый элемент 64-й степени этой матрицы -

1474472506836676237371358967075549167865631190000000000000000000000

что подтверждает мой ответ.

вычислить мощности матрицы эффективно

чтобы фактически вычислить 64-ю степень этой матрицы, самым простым подходом было бы повторное возведение в квадрат: После возведения в квадрат матрицы 6 раз у вас есть показатель 26 = 64. Если в некоторых другой сценарий ваш показатель (т. е. максимальная длина строки) не является степенью двух, вы все равно можете выполнить возведение в квадрат путем умножения соответствующих квадратов в соответствии с битовым шаблоном экспоненты. Вот что заставляет этот подход принимать O (log n) арифметические операции для вычисления результата для длины строки n, предполагая фиксированное число состояний и, следовательно, фиксированную стоимость для каждого квадратуры матрицы.

пример с детерминированный автомат

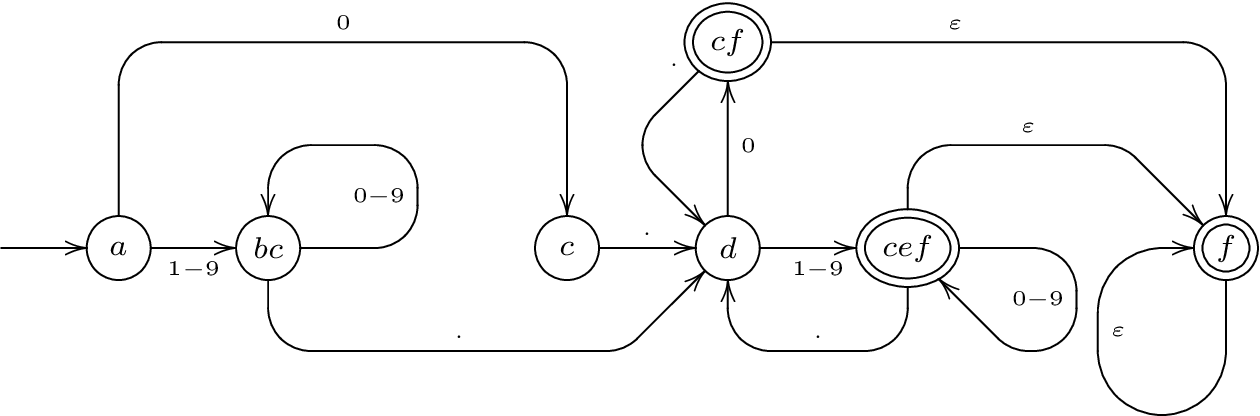
если бы вы сделали мой автомат детерминированным, используя обычную конструкцию powerset, вы бы в конечном итоге

Determinisitic Finite State Automaton

и сортировка состояний как a, bc, c, d, cf, cef, f можно было бы сделать матрицу перехода

⎛ 0  0  0  0  0  0  0⎞
⎜ 9 10  0  0  0  0  0⎟
⎜ 1  0  0  0  0  0  0⎟
⎜ 0  1  1  0  1  1  0⎟
⎜ 0  0  0  1  0  0  0⎟
⎜ 0  0  0  9  0 10  0⎟
⎝ 0  0  0  0  1  1  1⎠

и смогл суммировать последние 3 элемента первого столбца своего 64-я степень, чтобы получить тот же результат, что и выше.

9

один компонент

начните с поиска способов формирования одного компонента. Соответствующее регулярное выражение для одного компонента

0|[1-9][0-9]*

таким образом, это либо ноль, либо ненулевая цифра, за которой следует произвольное множество нулевых цифр. (Сначала я пропустил возможный случай единственного нуля, но комментарий Малата заставил меня осознать это.) Если общая длина такого компонента должна быть n, а вы пишите h(n) для обозначения количества способов формирования такой составляющей длины ровно n, тогда вы можете вычислить это h(n) как

h(n) = if n = 1 then 10 else 9 * 10^(n - 1)

здесь n = 1 случай учитывает все возможные числа, и другие случаи обеспечивают ненулевую первую цифру.

один или несколько компонентов

подраздел 9.1 только пишет, что UID-это куча чисел, разделенных точкой компоненты, как указано выше. Так что в регулярных выражениях это будет

(0|[1-9][0-9]*)(\.(0|[1-9][0-9]*))*

предположим f(n) - это количество способов написать UID длины n. Тогда у вас есть

f(n) = h(n) + sum h(i) * f(n-i-1) for i from 1 to n-2

первый член описывает случай одного компонента, в то время как сумма заботится о случае, когда она состоит из более чем одного компонента. В этом случае у вас есть первый компонент length я, затем точка, которая учитывает для -1 в Формуле, а затем оставшиеся цифры образуют один или несколько компонентов, которые выражаются рекурсивным использованием f.

два или более компонентов

как указано в комментарии cneller, часть раздела 9 перед подразделом 9.1 указывает, что должно быть по крайней мере два компонента. Таким образом, правильное регулярное выражение было бы больше похоже на

(0|[1-9][0-9]*)(\.(0|[1-9][0-9]*))+

С + в конце, указывающий, что мы хотим, по крайней мере, один повторение выражения в скобках. Получение выражения для этого просто означает, что в определении f:

g(n) = sum h(i) * f(n-i-1) for i from 1 to n-2

если суммировать все g(n) для n от 3 (минимально возможная длина UID) до 64 вы получаете количество возможных uid как

1474472506836676237371358967075549167865631190000000000000000000000

или около 1.5e66. Что значительно меньше, чем 4.5e66 вы получаете от вашего вычисление, с точки зрения абсолютной разницы, хотя это определенно на том же порядке величины. Кстати, ваша оценка явно не упоминает UIDs короче 64, но вы всегда можете рассмотреть возможность заполнения их точками в вашей настройке. Я сделал вычисление, используя несколько строк кода Python:

f = [0]
g = [0]
h = [0, 10] + [9 * (10**(n-1)) for n in range(2, 65)]
s = 0
for n in range(1, 65):
    x = 0
    if n >= 3:
        for i in range(1, n - 1):
            x += h[i] * f[n-i-1]
    g.append(x)
    f.append(x + h[n])
    s += x
print(h)
print(f)
print(g)
print(s)
9