Вычислить max draw down с помощью векторизованного решения в python
Максимальная Просадка является общей метрикой риска, используемой в количественном финансировании для оценки наибольшей отрицательной прибыли, которая была испытана.
недавно я стал нетерпеливым со временем, чтобы рассчитать максимальную просадку, используя мой циклический подход.
def max_dd_loop(returns):
"""returns is assumed to be a pandas series"""
max_so_far = None
start, end = None, None
r = returns.add(1).cumprod()
for r_start in r.index:
for r_end in r.index:
if r_start < r_end:
current = r.ix[r_end] / r.ix[r_start] - 1
if (max_so_far is None) or (current < max_so_far):
max_so_far = current
start, end = r_start, r_end
return max_so_far, start, end
Я знаком с общим восприятием того, что векторизованное решение было бы лучше.
вопросы:
- могу ли я векторизовать это проблема?
- как выглядит это решение?
- насколько это выгодно?
редактировать
Я изменил ответ Александра на следующую функцию:
def max_dd(returns):
"""Assumes returns is a pandas Series"""
r = returns.add(1).cumprod()
dd = r.div(r.cummax()).sub(1)
mdd = dd.min()
end = dd.argmin()
start = r.loc[:end].argmax()
return mdd, start, end
3 ответов
df_returns предполагается, что это фрейм данных возвратов, где каждый столбец является отдельной стратегией / менеджером / безопасностью, а каждая строка-новой датой (например, ежемесячно или ежедневно).
cum_returns = (1 + df_returns).cumprod()
drawdown = 1 - cum_returns.div(cum_returns.cummax())
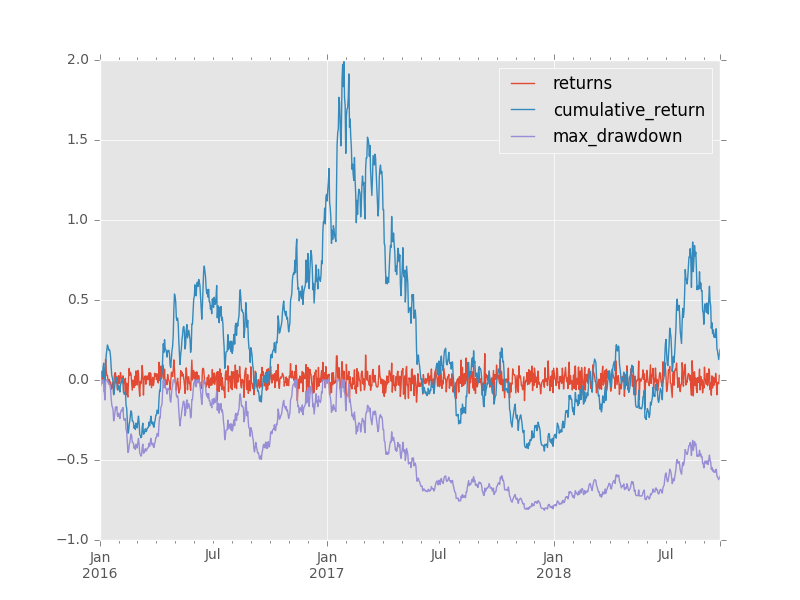
я сначала предложил использовать .expanding() окно, но это, очевидно, не обязательно с .cumprod() и .cummax() встроенные модули для расчета максимальной просадки до любой заданной точке:
df = pd.DataFrame(data={'returns': np.random.normal(0.001, 0.05, 1000)}, index=pd.date_range(start=date(2016,1,1), periods=1000, freq='D'))
df = pd.DataFrame(data={'returns': np.random.normal(0.001, 0.05, 1000)},
index=pd.date_range(start=date(2016, 1, 1), periods=1000, freq='D'))
df['cumulative_return'] = df.returns.add(1).cumprod().subtract(1)
df['max_drawdown'] = df.cumulative_return.add(1).div(df.cumulative_return.cummax().add(1)).subtract(1)
returns cumulative_return max_drawdown
2016-01-01 -0.014522 -0.014522 0.000000
2016-01-02 -0.022769 -0.036960 -0.022769
2016-01-03 0.026735 -0.011214 0.000000
2016-01-04 0.054129 0.042308 0.000000
2016-01-05 -0.017562 0.024004 -0.017562
2016-01-06 0.055254 0.080584 0.000000
2016-01-07 0.023135 0.105583 0.000000
2016-01-08 -0.072624 0.025291 -0.072624
2016-01-09 -0.055799 -0.031919 -0.124371
2016-01-10 0.129059 0.093020 -0.011363
2016-01-11 0.056123 0.154364 0.000000
2016-01-12 0.028213 0.186932 0.000000
2016-01-13 0.026914 0.218878 0.000000
2016-01-14 -0.009160 0.207713 -0.009160
2016-01-15 -0.017245 0.186886 -0.026247
2016-01-16 0.003357 0.190869 -0.022979
2016-01-17 -0.009284 0.179813 -0.032050
2016-01-18 -0.027361 0.147533 -0.058533
2016-01-19 -0.058118 0.080841 -0.113250
2016-01-20 -0.049893 0.026914 -0.157492
2016-01-21 -0.013382 0.013173 -0.168766
2016-01-22 -0.020350 -0.007445 -0.185681
2016-01-23 -0.085842 -0.092648 -0.255584
2016-01-24 0.022406 -0.072318 -0.238905
2016-01-25 0.044079 -0.031426 -0.205356
2016-01-26 0.045782 0.012917 -0.168976
2016-01-27 -0.018443 -0.005764 -0.184302
2016-01-28 0.021461 0.015573 -0.166797
2016-01-29 -0.062436 -0.047836 -0.218819
2016-01-30 -0.013274 -0.060475 -0.229189
... ... ... ...
2018-08-28 0.002124 0.559122 -0.478738
2018-08-29 -0.080303 0.433921 -0.520597
2018-08-30 -0.009798 0.419871 -0.525294
2018-08-31 -0.050365 0.348359 -0.549203
2018-09-01 0.080299 0.456631 -0.513004
2018-09-02 0.013601 0.476443 -0.506381
2018-09-03 -0.009678 0.462153 -0.511158
2018-09-04 -0.026805 0.422960 -0.524262
2018-09-05 0.040832 0.481062 -0.504836
2018-09-06 -0.035492 0.428496 -0.522411
2018-09-07 -0.011206 0.412489 -0.527762
2018-09-08 0.069765 0.511031 -0.494817
2018-09-09 0.049546 0.585896 -0.469787
2018-09-10 -0.060201 0.490423 -0.501707
2018-09-11 -0.018913 0.462235 -0.511131
2018-09-12 -0.094803 0.323611 -0.557477
2018-09-13 0.025736 0.357675 -0.546088
2018-09-14 -0.049468 0.290514 -0.568542
2018-09-15 0.018146 0.313932 -0.560713
2018-09-16 -0.034118 0.269104 -0.575700
2018-09-17 0.012191 0.284576 -0.570527
2018-09-18 -0.014888 0.265451 -0.576921
2018-09-19 0.041180 0.317562 -0.559499
2018-09-20 0.001988 0.320182 -0.558623
2018-09-21 -0.092268 0.198372 -0.599348
2018-09-22 -0.015386 0.179933 -0.605513
2018-09-23 -0.021231 0.154883 -0.613888
2018-09-24 -0.023536 0.127701 -0.622976
2018-09-25 0.030160 0.161712 -0.611605
2018-09-26 0.025528 0.191368 -0.601690
учитывая временной ряд возвратов, нам нужно оценить совокупный доход для каждой комбинации начальной и конечной точек.
первый трюк заключается в преобразовании временного ряда возвратов в ряд индексов возврата. Учитывая ряд индексов возврата, я могу рассчитать возврат за любой подпериод с индексом возврата в начале ri_0 и в конце ri_1. Расчет: ri_1 / ri_0 - 1.
второй фокус в том, чтобы произвести вторую серию инверсии индексов возврата. Если r - мой ряд возвращаемых индексов, то 1 / r-мой ряд инверсий.
третий трюк-взять матричное произведение r * (1 / r).Транспонировать.
r-матрица N x 1. (1 / r).Транспонирование-это матрица 1 x n. Полученный продукт содержит все комбинации ri_j / ri_k. Просто вычтите 1,и у меня действительно есть возврат.
четвертый трюк заключается в том, чтобы убедиться, что я ограничиваю свой знаменатель для представления периодов до те, которые представлены числителем.
ниже-это моя функция векторизации.
import numpy as np
import pandas as pd
def max_dd(returns):
# make into a DataFrame so that it is a 2-dimensional
# matrix such that I can perform an nx1 by 1xn matrix
# multiplication and end up with an nxn matrix
r = pd.DataFrame(returns).add(1).cumprod()
# I copy r.T to ensure r's index is not the same
# object as 1 / r.T's columns object
x = r.dot(1 / r.T.copy()) - 1
x.columns.name, x.index.name = 'start', 'end'
# let's make sure we only calculate a return when start
# is less than end.
y = x.stack().reset_index()
y = y[y.start < y.end]
# my choice is to return the periods and the actual max
# draw down
z = y.set_index(['start', 'end']).iloc[:, 0]
return z.min(), z.argmin()[0], z.argmin()[1]
как это работает?
для векторизованного решения я провел 10 итераций по временным рядам длин [10, 50, 100, 150, 200]. Время, которое потребовалось, ниже:
10: 0.032 seconds
50: 0.044 seconds
100: 0.055 seconds
150: 0.082 seconds
200: 0.047 seconds
тот же тест для зацикленного решения ниже:
10: 0.153 seconds
50: 3.169 seconds
100: 12.355 seconds
150: 27.756 seconds
200: 49.726 seconds
редактировать
ответ Александра дает превосходные результаты. Такой же тест используя измененный код
10: 0.000 seconds
50: 0.000 seconds
100: 0.004 seconds
150: 0.007 seconds
200: 0.008 seconds
Я изменил его код на следующую функцию:
def max_dd(returns):
r = returns.add(1).cumprod()
dd = r.div(r.cummax()).sub(1)
mdd = drawdown.min()
end = drawdown.argmin()
start = r.loc[:end].argmax()
return mdd, start, end