Вычислительная геометрия, тетраэдр подписанный том
Я не уверен, если это правильное место, чтобы спросить, но здесь идет...
короткая версия: Я пытаюсь вычислить ориентацию треугольника на плоскости, образованной пересечением 3 ребра, без явного вычисления точек пересечения.
версия: мне нужно триангулировать PSLG на треугольнике в 3D. Вершины PSLG определяются пересечениями отрезков линии с плоскостью через треугольник и являются гарантированно лежит внутри треугольника. Предполагая, что у меня есть точки пересечения, я мог бы проецировать в 2D и использовать тест точки-линии-стороны (или треугольника), чтобы определить ориентацию треугольника между любыми 3 точками пересечения.
проблема в том, что я не могу явно вычислить точки пересечения из-за ошибки с плавающей запятой, которая накапливается, когда я нахожу пересечение линии и плоскости. Чтобы выяснить, поражают ли сегменты линии треугольник в первую очередь, я использую некоторые свободно доступные надежные геометрические предикаты, которые дают знак объема тетраэдра или эквивалентно, на какой стороне плоскости лежит точка. Я могу определить, находятся ли конечные точки отрезка линии на противоположных сторонах плоскости через треугольник, а затем сформировать тетраэдры между отрезком линии и каждым краем треугольника, чтобы определить, находится ли точка пересечения внутри треугольника.
поскольку я не могу явно вычислить точки пересечения, мне интересно, если существует способ выразить тот же расчет 2D-ориентации в 3D, используя только исходные точки. Если есть 3 ребра, поражающие треугольник, который дает мне 9 очков в общей сложности, чтобы играть. Предполагая, что то, что я прошу, даже возможно (используя только тесты 3D orient), то я предполагаю, что мне нужно будет сформировать некоторое подмножество всех возможных тетраэдров между этими 9 точками. Мне трудно даже представить это, не говоря уже о том, чтобы перегнать его в формулу или код. Я даже не могу google это, потому что я не знаю, какая стандартная терминология может быть для этого типа проблем.
есть идеи, как это сделать? Спасибо. Возможно, мне также следует спросить MathOverflow...
EDIT: после прочтения некоторых комментариев, одна вещь, которая приходит мне в голову... Возможно, если бы я мог поместить неперекрывающиеся тетраэдры между тремя сегментами линии, то ориентация любого из тех, которые пересекли плоскость, была бы ответом, который я ищу. Кроме случаев, когда ребра заключают простая треугольная призма, я не уверен, что эта подзадача также разрешима.
EDIT: запрошенное изображение.
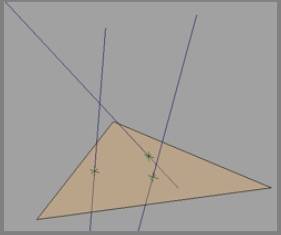
4 ответов
Я отвечаю на это как на MO & SO, расширяя комментарии, которые я сделал на MO.
мое чувство заключается в том, что никакой вычислительный трюк с подписанными томами тетраэдров не позволит избежать проблем точности, которые являются вашей главной заботой. Это потому, что, если у вас плотно скрученные сегменты, ориентация треугольника зависит от точного позиционирования плоскости резания.
[изображения удалены, см. ниже]
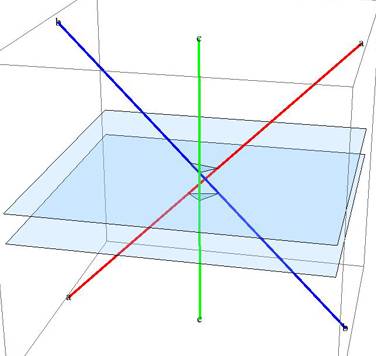
В приведенном выше примере, верхняя плоскость пересекает отрезков в порядке (a, b, c) [ccw сверху]: (красный,синий,зеленый), в то время как нижняя плоскость пересекается в обратном порядке (c, b, A): (зеленый,синий,красный). Высота
плоскость резания может быть определена вашим последним битом точности.
следовательно, я думаю, что имеет смысл просто идти вперед и вычислять точки пересечения в плоскость вырезывания, используя достаточную точность для того чтобы сделать вычисление точным. Если координаты конечных точек сегмента и коэффициентов самолета L биты точности, тогда необходимо только небольшое увеличение постоянного фактора. Хотя я точно не знаю, что это за фактор, он невелик-возможно, 4. Вам не понадобится, например,L2 бит, потому что вычисление решает линейные уравнения. Таким образом, не будет взрыва в точности, необходимой для точного вычисления этого.
удачи!
(Я не отправляю потому что у меня нет репутации. Видеть the ответ МО.)
редактировать: видите ответ MO, но вот изображение:
Я бы написал символические векторные уравнения, вы знаете, с точечными и перекрестными произведениями, чтобы найти Нормаль треугольника пересечения. Затем знак точечного произведения этой нормали с начальным треугольником дает ориентацию. Итак, наконец, вы можете выразить это в знаке формы (F (p1,...,p9)), где p1-p9-ваши точки, А F () - уродливая формула, включающая точки и перекрестные произведения различий (pi-pj). Не знаю, можно ли это сделать проще, но этот общий подход делает работа.
как я понимаю, у вас есть три линии, пересекающие плоскость, и вы хотите рассчитать ориентацию треугольника, образованного точками пересечения, без расчета самих точек пересечения?
если это так: у вас есть самолет
N·(x - x0) = 0
и шесть очков...
l1a, l1b, l2a, l2b, l3a, l3b
...образуя три линии
l1 = l1a + t(l1b - l1a) l2 = l2a + u(l2b - l2a) l3 = l3a + v(l3b - l3a)
точки пересечения этих линий с плоскостью происходят при определенных значениях t, u, v, которые я буду называть tя, uя, vя
N·(l1a + ti(l1b - l1a) - x0) = 0
N·(x0 - l1a)
ti = ----------------
N·(l1b - l1a)
(similarly for ui, vi)
тогда конкретные точки пересечения являются
intersect1 = l1a + ti(l1b - l1a) intersect2 = l2a + ui(l2b - l2a) intersect3 = l3a + vi(l3b - l3a)
наконец, ориентация вашего треугольника
orientation = direction of (intersect2 - intersect1)x(intersect3 - intersect1)
(x является кросс-продуктом) работайте в обратном направлении, подключая значения, и у вас будет уравнение для ориентации, основанное только на N, x0, и свои шесть очков.
давайте назовем ваши вершины треугольника T[0], T[1], T[2], а конечными точками сегмента первой строки являются L[0] и L[1], второй -L[2] и L[3], третья -L[4] и L[5]. Я полагаю, вы хотите функцию
int Orient(Pt3 T[3], Pt3 L[6]); // index L by L[2*i+j], i=0..2, j=0..1
который возвращает 1, Если пересечения имеют ту же ориентацию, что и треугольник, и -1 в противном случае.
Результат должен быть симметричным при обмене j значения, антисимметричные при обмене i значения и T индексы. Пока вы можете вычислить количество с помощью этих симметрий, это все, что вам нужно.
попробуем
Sign(Product( Orient3D(T[i],T[i+1],L[2*i+0],L[2*i+1]) * -Orient3D(T[i],T[i+1],L[2*i+1],L[2*i+0]) ), i=0..2))
где произведение должно быть взято над циклическими перестановками индексов (по модулю 3). Я считаю, что это имеет все необходимые свойства симметрии. Orient3D это 4-точечный тест ориентации плоскости Шевчука, который, я полагаю, вы используете.
