Зачем нам нужен единичный вектор (другими словами, Зачем нам нужно нормализовать векторы)?
Я читаю книгу об игре AI.
один из терминов, который используется для нормализации вектора, который должен превратить вектор в единицу. Для этого вы должны разделить каждое измерение x, y и z по его величине.
мы должны превратить вектор в единицу, прежде чем что-либо с ним делать. Почему?
и может ли кто-нибудь дать некоторые сценарии, где мы должны использовать единичный вектор?
спасибо!
5 ответов
вам не нужно нормализовать векторы, но это делает много уравнений немного проще, когда вы это делаете. Это также может сделать API меньше: любая форма стандартизации может уменьшить количество необходимых функций.
вот простой пример. Предположим, вы хотите найти угол между двумя векторами u и v. Если они являются единичными векторами, угол - это просто arccos (uv). Если это не единичные векторы, угол равен arccos (uv| (|u| / v/)). В таком случае, вы в конечном итоге вычисление норм u и v в любом случае.
Как говорит Джон Д. Кук-в основном вы делаете это, потому что вы заботитесь о направлении, а не о самом векторе. В зависимости от контекста вы, скорее всего, не хотите / не нуждаетесь в информации о величине - только в самом направлении. Вы нормализуете, чтобы удалить величину, чтобы она не искажала другие вычисления, что, в свою очередь, упрощает многие другие вещи.
в терминах AI - представьте, что вы берете вектор V между P1 (плохой парень AI) и P2 (ваш герой) в качестве направления для плохой парень, чтобы двигаться. Вы хотите, чтобы плохой парень двигался со скоростью N в такт - как вы это вычисляете? Ну, мы либо нормализуем вектор каждый такт, умножаем на N, чтобы выяснить, как далеко они продвинулись, либо предварительно нормализуем направление в первую очередь, и просто умножаем единичный вектор на N каждый раз-иначе плохой парень двигался бы дальше, если бы он был дальше от героя! Если герой не меняет позу, это на один расчет меньше, чтобы беспокоиться.
в этом контекст, это не имеет большого значения - но что, если у вас есть сто плохих парней? Или тысячу? Что делать, если ваш ИИ должен иметь дело с комбинациями плохих парней? Внезапно вы экономите сотню или тысячу нормализаций за каждый удар. Поскольку это несколько умножений и квадратный корень для каждого, в конечном итоге вы достигнете точки, где не нормализация данных раньше времени означает, что вы собираетесь убить скорость обработки ИИ.
более широко-математика для этого действительно распространена - люди делая здесь то, что они делают для таких вещей, как 3D - рендеринг-если бы вы не объединяли, например, нормали для своих поверхностей, у вас были бы потенциально тысячи нормализаций на рендеринг, которые совершенно не нужны. У вас есть два варианта: один - заставить каждую функцию выполнить расчет, или два - предварительно нормализовать данные.
с точки зрения дизайнера фреймворка: последний по своей сути быстрее - если мы предполагаем первое, даже если ваш пользователь думает нормализовать данные, им придется пройти ту же процедуру нормализации, или вам придется предоставить две версии каждой функции, что является головной болью. Но в тот момент, когда вы заставляете людей думать о том, какую версию функции вызывать, вы можете также заставить их думать достаточно, чтобы вызвать правильный, и только предоставить его в первую очередь, заставляя их делать правильные вещи для производительности.
вы часто нормализуете вектор, потому что вы заботитесь только о направлении векторных точек, а не о величине.
конкретный сценарий Нормальное Отображение. Комбинируя свет, падающий на поверхность, и векторы, перпендикулярные поверхности, вы можете создать иллюзию глубины. Векторы с поверхности определяют параллельное направление, а величина вектора фактически делает вычисления неправильными.
мы должны превратить вектор в единицы прежде чем мы что-нибудь с ним сделаем.
Это утверждение неверно. Все векторы не являются единичными векторами.
векторы, которые образуют основу для координатного пространства, имеют два очень хороших свойства, которые облегчают их работу:
- они ортогональных
- они единичные векторы-величина = 1
Это позволяет записать любой вектор в 3D-пространстве как линейная комбинация единичных векторов:
alt текст http://www.equationsheet.com/latexrender/pictures/e691d8878d3d2cf83362af36faa16096.gif
Я могу выбрать, чтобы превратить этот вектор в единичный вектор, если мне нужно, разделив каждый компонент на величину
alt текст http://www.equationsheet.com/latexrender/pictures/78a0af48a0d02492fdd2b5377157c6a8.gif
Если вы не знаете, что координата пространства или основы векторы, я бы рекомендовал узнать немного больше о математике графики, прежде чем идти намного дальше.
в дополнение к уже представленным ответам я бы упомянул два важных аспекта.
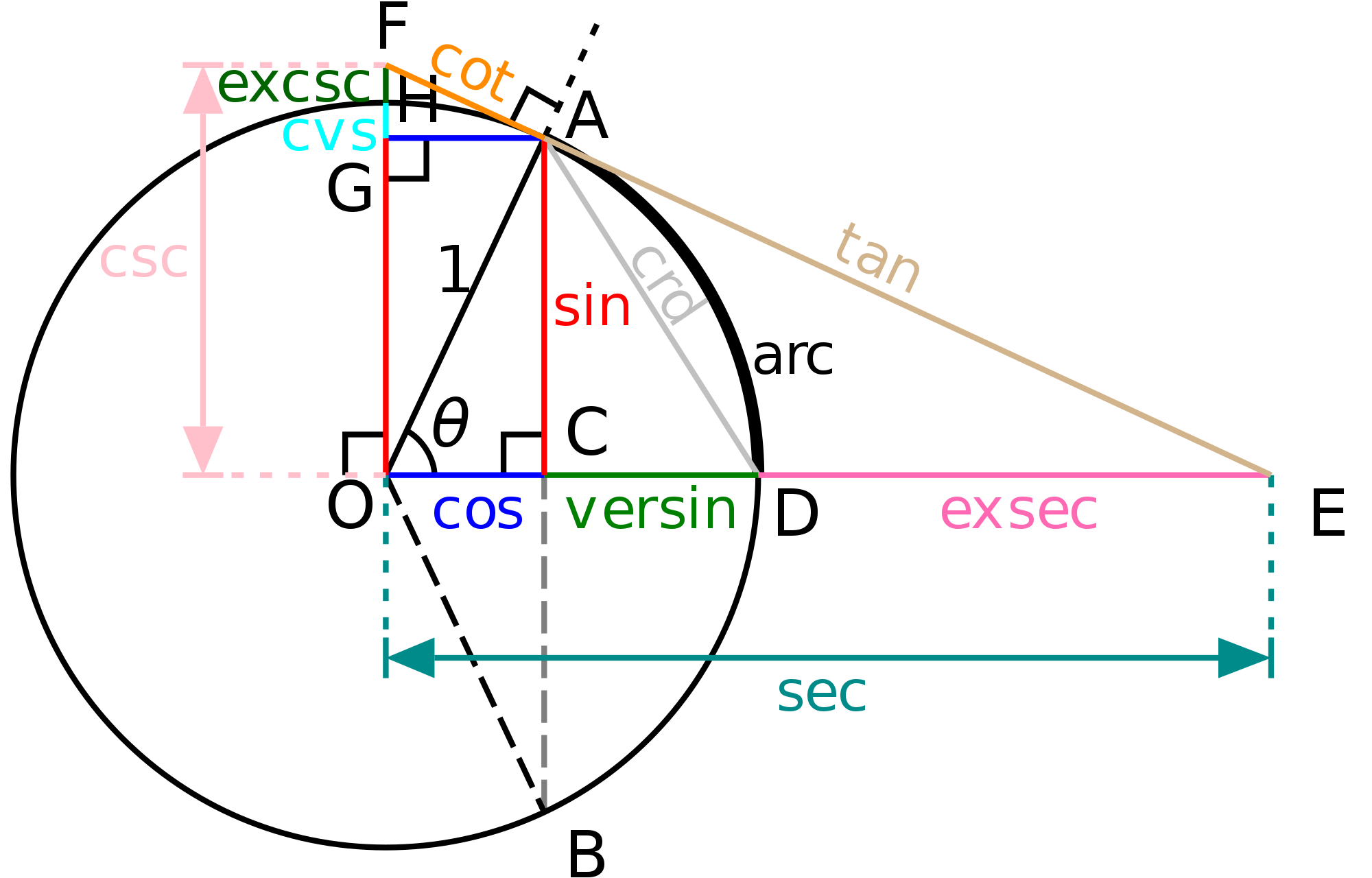
тригонометрия определяется на единичной окружности
все тригонометрические функции определяются по единичной окружности. Число pi сам определяется по единичной окружности.
при нормализации векторов можно использовать все тригонометрические функции напрямую, без каких-либо раундов масштабирования. Как упоминалось ранее, угол между двумя векторами блок просто: acos(dot(u, v)), без дальнейшего масштабирования.
единичные векторы позволяют отделить величину от направления
вектор можно интерпретировать как величину, несущую два типа информации: величину и направление. Важными примерами являются сила, скорость и ускорение.
если вы хотите заниматься отдельно С величиной и направлением, представление формы vector = magnitude * direction, где magnitude является скаляром и direction единичный вектор, часто очень удобен: изменения величины влекут за собой скалярные манипуляции, а изменения направления не изменяют величину. The direction должен быть единичный вектор, чтобы гарантировать, что величина vector равен magnitude.