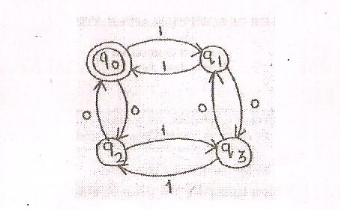
Нужно регулярное выражение для конечных автоматов: четное число 1s и четное число 0s
моя проблема может звучать по-другому для вас.
Я новичок, и я изучаю конечные автоматы. Я googing через Интернет, чтобы найти Регулярное выражение для конечных автоматов данной машины ниже.
может ли кто-нибудь помочь мне написать "регулярное выражение для конечных автоматов" вышеуказанной машины
любая помощь будет оценена
2 ответов
Как написать регулярное выражение для DFA с помощью теоремы Ардена
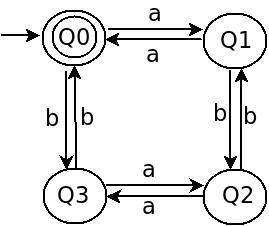
позволяет вместо языковых символов 0,1 взять Σ = {a, b} и следующее-Новый DFA.
Уведомление государственного старт м0
вы не дали, но в моем ответе начальное состояние Q0, где конечное состояние также Q0.
язык, принятый is DFA, установлен из всех строки состоят из символов a и b где количество символов a и b еще (в том числе Λ).
пример строки {Λ, aa, bb, abba, babbab }, нет ограничения порядка и скороговорки появления символа просто оба должны быть четным количеством времени.
Примечание: Λ разрешено, потому что число(a) и numberOf (b) равен нулю, что даже.
как я уже сказал в моем строчке ответ:Как написать регулярное выражение для DFA каждое государство хранит некоторую информацию. Ниже приведена информация о том, какая информация хранится в каждом состоянии выше DFA.
Q0: четное число
aи даже количествоb
Q1: нечетное числоaи даже количествоb
Q2: нечетное числоaи нечетное числоb
Q3: четное числоaи нечетное числоb
(вы можете сделать DFAs для более интересных языков, изменив набор конечных насыщений)
следует прочитать выровненный ответ, потому что мой подход к оштрафованному RE для DFA в обоих ответах отличается
что такое обычный Выражение?
Подход ниже объясняется с помощью Арден терм, может применяться на диаграмме перехода, в которой есть одно начальное состояние и нет никакого нулевого перемещения (наш DFA находится в этой форме). Эту технику объясняют в книге:--143-->Формальные Языки И Теория Автоматов
помните 4.2 ТЕОРЕМА АРДЕНА:
пусть
BиCbe-это два регулярных выраженияΣ. ЕслиCне содержитΛ, то для уравнения A = B + AC имеет единственное (одно и только одно) решение A = BC*.
[решение]:
Шаг 1: напишите начальное уравнение, одно уравнение для соответствующего каждому состоянию в DFA. Это уравнение означает, как состояние может быть достигнуто за один шаг
таким образом, согласно нашему DFA возможны следующие 4-уравнения:
- Q0 =
Λ+ Q1a + Q3b- Q1 = Q0a + Q2b
- Q2 = Q1b + Q3a
- Q3 = Q0b + Q2a
в уравнении (1) extra Λ потому что Q0 начальный состояние, может быть достигнуто без какого-либо ввода (точка начала).
Потому Что Q0 также является только конечным состоянием, строка состоит из a, b приемлемо, если он заканчивается на Q0. Значение Q0 даст нам требуемое регулярное выражение, поэтому наша цель-просто уравнение-(1) в терминах a, b.
Шаг 2: упростите уравнение, используя значение состояний из других уравнений и используя Упрощенное уравнение Ардена.
давайте сначала возьмем уравнение-(4) и заменим значение Q2 из уравнения(3).
Q3 = Q0b + Q2a
Q3 = Q0b + (Q1b + Q3a) a
Q3 = Q0b + Q1ba + Q3aa
последнее уравнение можно просмотреть в виде уравнения Ардена A = B + AC. Где A-Q3, B = Q0b + Q1ba и C = aa. Итак, согласно Терму Ардена, уравнение Q3 = Q0b + Q1ba + Q3aa имеет уникальное решение, которое:
Q3 = (Q0b + Q1ba)(aa)*
или можно написать это следующим образом:
5.Q3 = Q0b (aa)* + Q1ba (aa)*
логически вы можете проверить / понять eq - (5) означает Q3 может быть достигнуто двумя способами (+) кулак от подачи b на Q0 тогда есть петля с меткой aa на Q3, второй путь от Q1 с применение ba.
аналогичным образом, мы можем упростить уравнение(2)
Q1 = Q0a + Q2b
Q1 = Q0a + (Q1b + Q3a) b
Q1 = Q0a + Q1bb + Q3ab
используйте здесь правила упрощения Ардена.
Q1 = (Q0a + Q3 ab) (bb)*
дальнейшее упрощение
6.Q1 = Q0a (bb)* + Q3ab (bb)*
теперь значение Q3 из уравнения(5) в уравнение(6)
Q1 = Q0a (bb)* + (Q0b (aa)* + Q1ba (aa)*) ab(bb)*
Q1 = Q0a (bb)* + Q0b(aa)* ab (bb)* + Q1ba( aa)* ab(bb)*
снова улучшите это последнее уравнение, используя закон упрощения Ардена.
Q1 = (Q0a (bb)* + Q0b( aa)* ab(bb)*) (ba(aa)* ab(bb)*)*
принять Q0 аферист:
7.Q1 = Q0(a (bb)* + b(aa)* ab(bb)*) (ba(aa)* ab(bb)*)*
можете ли вы понять это уравнение, его, как вы можете перейти к Q1 из состояния Q0? Мы помним это решение в уравнение(7)
как указано выше, мы можем оценить значение Q1 в терминах состояния Q0 и a, b, аналогично мы должны оценить значение для состояния Q3. Для этого мы можем просто поставить значение состояния Q1 из уравнения(5) в уравнение(7).
5.Q3 = Q0b (aa)* + Q1ba (aa)*.Q3 = Q0b (aa)* + Q0(a (bb)* + b(aa)* ab(bb)*) (ba(aa)* ab(bb)*)*ba(aa)*8.Q3 = Q0 (b (aa)* + (a(bb)* + b(aa)* ab(bb)*) (ba(aa)* ab(bb)*)* ba(aa)*)
теперь в уравнении (1) поставьте значение состояния Q3 и Q1 из числа уравнений (8) и (7) восприимчиво.
Q0 =
Λ+ Q1a + Q3b
Q0 =Λ+ Q0(a (bb)* + (aa)* ab(bb)* ) (ba (aa)* ab(bb)*) * a + Q0 (b (aa)* + (a(bb)* + b(aa)* ab(bb)*) (ba(aa)* ab(bb)*)* ba(aa)*) B
теперь, в последний раз применить решение Arden, чтобы найти значение состояния Q0 в терминах символов a и b.
Q0 =
Λ+ ((a (bb) * + (aa)* ab (bb)* ) (ba (aa) * ab (bb)* ) * a + (b (aa) * + (a (bb) * + b(aa)* ab (bb)*) (ba(aa)* ab(bb)* )* ba (aa)* ) b )*
это то же самое, что (мы можем отбросить Λ здесь) RE:
((a (bb) * + (aa)* ab (bb)*) (ba(aa)* ab ( bb)* )* a + (b (aa)* + (a(bb)* + b(aa)* ab (bb)*) (ba(aa)* ab(bb)* )* ba (aa)* ) b )*
это тот огонь, который вы ищете.
я не уверен, что это можно упростить. Я оставляю это как упражнение для тебя.
в связанном вопросе я предложил неформальный и аналитический но было трудно применить и найти RE для этого DFA, и этот вопрос демонстрирует силу теоремы Ардена и пошаговое решение.
Edit:
мое предыдущее регулярное выражение корректно, но трудно для винограда, потому что несимметричная форма. Ниже я пишу новую форму RE, которая более симметрична.
мы имеем уравнение - (5), (6) следующим образом:
5.Q3 = Q0b (aa)* + Q1ba (aa)*6.Q1 = Q0a (bb)* + Q3ab (bb)*
оба симметричны в конструкции и легки для того чтобы выучить. (прочитайте мой комментарий после eq - (5) выше)
оценить значение состояния Q1 в терминах Q0, я поставил значение Q3 из уравнения(5) в уравнение(6), что дает мне уравнение(7) следующим образом:
7.Q1 = Q0(a (bb)* + b(aa)* ab(bb)*) (ba(aa)* ab(bb)*)*
аналогично, чтобы оценить значение состояния Q3 в терминах Q0, мы можем поставить значение Q1 из уравнения(6) в уравнение(5), что даст нам новую форму уравнением(8) следующим образом:
Q3 = Q0b (aa)* + Q1ba (aa)*
Q3 = Q0b (aa)* + (Q0a (bb)* + Q3 ab(bb)* ) ba (aa)*
Q3 = Q0b (aa)* + Q0a(bb)* ba (aa)* + Q3 ab(bb)* ba (aa)*
теперь мы можем получить уравнение - (8) в желаемой форме:
8.Q3 = Q0(b (aa)* + a(bb)* ba(aa)*) (ab(bb)* ba(aa)*)*
теперь у нас есть уравнение-(1), (7), (8):
1.Q0 =Λ+ Q1a + Q3b7.Q1 = Q0(a (bb)* + b(aa)* ab(bb)*) (ba(aa)* ab(bb)*)*8.Q3 = Q0(b (aa) * + a( bb) * ba (aa)*) (ab (bb)* ba(aa)* )*
теперь мы можем получить уравнение - (8) в желаемой форме:
8.Q3 = Q0(b (aa)* + a(bb)* ba(aa)*) (ab(bb)* ba(aa)*)*
теперь у нас есть уравнение-(1), (7), (8):
1.Q0 =Λ+ Q1a + Q3b7.Q1 = Q0(a (bb)* + b(aa)* ab (bb)*) (ba(aa)* ab (bb)*)*8.Q3 = Q0(b (aa)* + a(bb)* ba(aa)*) (ab(bb)* ba(aa)*)*
теперь поставьте значение состояния Q1 и Q3 в уравнение(1):
Q0 =
Λ+ Q0(a(bb)* + b(aa)* ab (bb)*) (ba(aa)* ab (bb)* )* a + Q0(b (aa) * + a( bb) * ba (aa)*) (ab (bb)* ba (aa)*) * b
также можно записать как:
Q0 =
Λ+ Q0 ((a (bb) * + b( aa)* ab(bb)*) (ba(aa)* ab(bb)*)* a + (b(aa)* + a(bb)* ba(aa)*) (ab(bb)* ba(aa)*) * B)
затем примените теорему Ардена к этому уравнению, и мы получим окончательный RE:
регулярное выражение для четных чисел 'a' и четных чисел 'b':
((a (bb) * + b( aa) * ab (bb)* ) (ba( aa) * ab (bb)*) * a + (b (aa) * + a (bb) * ba (aa)*) (ab(bb)* ba (aa)* )* B)
может ли еще один шаг упростить, как показано ниже:
((a + b(aa)*ab)(bb)*(ba(aa)*ab(bb)*)*a + (b + a(bb)*ba)(aa)*(ab(bb)*ba(aa)*)*b)*
пусть E-это язык с четным числом a и четным числом b, а ниже приведено регулярное выражение для языка E.
[00 + 11 + (01+10)(11+00)(01+10)]
00 = type1
11 = type2
(01+10)(00+11)*(01+10) = type3
предположим, что мы сканируем вдоль слова на языке E слева направо, читая буквы по две за раз. Сначала мы приходим к двойному 0 (type1), потом двойной 1 (type2), затем к другому двойному 0 (снова введите 1). Тогда, возможно, мы наткнемся на пару букв, которые не совпадают. Скажем, например, что следующие две буквы 10. Это должно начинаться с подстроки type3. Он начинается с undoubled пара (или 01 или 10), то есть раздел удвоенных букв (много повторений либо 00 или 11), а затем он, наконец, заканчивается с другой undoubled пара (либо 01, либо 10 раз). Одним из свойств этого раздела слова является то, что он имеет четное число 0 и четное число единиц. Если раздел начинался с 10, он мог заканчиваться 01, все еще давая два 0 и два 1 на концах с только удвоенными буквами между ними. Если это началось с 10 и закончил с 01, опять же, это даст четное число 0 и четное число единиц. После этого раздела type3 мы могли бы продолжить с большим количеством разделов типа или type2, пока мы не столкнулись с другим undoubled пара, начиная другой раздел type3. Мы знаем, что другой undoubled пара встанешь чтобы сбалансировать первоначальный. Суммарный эффект заключается в том, что каждое слово из языка E содержит четное число 0 и четное число на 1-х