Определить, перекрывают ли друг друга два прямоугольника?
Я пытаюсь написать программу на C++, которая принимает следующие входные данные от пользователя для создания прямоугольников (между 2 и 5): высота, ширина, х-поз и y-поз. Все эти прямоугольники будут существовать параллельно оси x и y, то есть все их ребра будут иметь наклоны 0 или бесконечности.
Я попытался реализовать то, что упоминается в этой вопрос, но мне не очень везет.
моя текущая реализация делает следующий:
// Gets all the vertices for Rectangle 1 and stores them in an array -> arrRect1
// point 1 x: arrRect1[0], point 1 y: arrRect1[1] and so on...
// Gets all the vertices for Rectangle 2 and stores them in an array -> arrRect2
// rotated edge of point a, rect 1
int rot_x, rot_y;
rot_x = -arrRect1[3];
rot_y = arrRect1[2];
// point on rotated edge
int pnt_x, pnt_y;
pnt_x = arrRect1[2];
pnt_y = arrRect1[3];
// test point, a from rect 2
int tst_x, tst_y;
tst_x = arrRect2[0];
tst_y = arrRect2[1];
int value;
value = (rot_x * (tst_x - pnt_x)) + (rot_y * (tst_y - pnt_y));
cout << "Value: " << value;
однако я не совсем уверен, что (a) я реализовал алгоритм, с которым я связался правильно, или если я сделал именно так, как интерпретировать это?
какие предложения?
21 ответов
if (RectA.Left < RectB.Right && RectA.Right > RectB.Left &&
RectA.Top > RectB.Bottom && RectA.Bottom < RectB.Top )
или, используя декартовы координаты
(при X1 быть левым coord, X2 быть правым coord, увеличивая слева направо и Y1 быть верхним coord, и Y2 быть нижним coord, увеличивая снизу вверх) ...
if (RectA.X1 < RectB.X2 && RectA.X2 > RectB.X1 &&
RectA.Y1 > RectB.Y2 && RectA.Y2 < RectB.Y1)
ПРИМЕЧАНИЕ: ДЛЯ ВСЕХ ПОЛЬЗОВАТЕЛЕЙ SO С ПОЛНОМОЧИЯМИ РЕДАКТИРОВАНИЯ. ПОЖАЛУЙСТА, ПРЕКРАТИ ВОЗИТЬСЯ С ЭТИМ.
скажем, у вас есть прямая кишка A и прямая кишка B. Доказательство от противного. Любое из четырех условий гарантирует, что никакое перекрытие не может exist:
- Cond1. Если левый край A находится справа от правого края B, - тогда A полностью справа от B
- Cond2. Если правый край A находится слева от левого края B, - тогда A полностью слева от B
- Cond3. Если верхний край A находится ниже нижнего края B, - тогда A полностью ниже B
- Cond4. Если нижний край A выше верхнего края B, - тогда A полностью выше Б
так условие для non-перекрытия
Cond1 Or Cond2 Or Cond3 Or Cond4
таким образом, достаточным условием для перекрытия наоборот.
Not (Cond1 Or Cond2 Or Cond3 Or Cond4)
закон де Моргана говоритNot (A or B or C or D) это то же самое, что Not A And Not B And Not C And Not D
Итак, используя De Morgan, мы имеем
Not Cond1 And Not Cond2 And Not Cond3 And Not Cond4
это эквивалентно:
- левый край A слева от правого края B, [
RectA.Left < RectB.Right] и - правый край A справа от левого края B, [
RectA.Right > RectB.Left], и - a сверху над B снизу, [
RectA.Top > RectB.Bottom] и - дно A ниже верхней части B [
RectA.Bottom < RectB.Top]
Примечание 1: очевидно, этот же принцип может быть распространен на любое число измерений.
примечание 2.: также должно быть довольно очевидно, чтобы считать перекрытия только одного пикселя, измените < и/или > на границе с <= или >=.
Примечание 3: это ответ, при использовании декартовых координат (X, Y) основан на стандартных алгебраических декартовых координатах (x увеличивается слева направо, а Y увеличивается снизу вверх). Очевидно, что там, где компьютерная система может механизировать координаты экрана по-разному (например, увеличивая Y сверху вниз или X справа налево), синтаксис должен быть соответствующим образом скорректирован/
struct rect
{
int x;
int y;
int width;
int height;
};
bool valueInRange(int value, int min, int max)
{ return (value >= min) && (value <= max); }
bool rectOverlap(rect A, rect B)
{
bool xOverlap = valueInRange(A.x, B.x, B.x + B.width) ||
valueInRange(B.x, A.x, A.x + A.width);
bool yOverlap = valueInRange(A.y, B.y, B.y + B.height) ||
valueInRange(B.y, A.y, A.y + A.height);
return xOverlap && yOverlap;
}struct Rect
{
Rect(int x1, int x2, int y1, int y2)
: x1(x1), x2(x2), y1(y1), y2(y2)
{
assert(x1 < x2);
assert(y1 < y2);
}
int x1, x2, y1, y2;
};
bool
overlap(const Rect &r1, const Rect &r2)
{
// The rectangles don't overlap if
// one rectangle's minimum in some dimension
// is greater than the other's maximum in
// that dimension.
bool noOverlap = r1.x1 > r2.x2 ||
r2.x1 > r1.x2 ||
r1.y1 > r2.y2 ||
r2.y1 > r1.y2;
return !noOverlap;
}
легче проверить, находится ли прямоугольник полностью вне другого, поэтому, если это либо
слева...
(r1.x + r1.width < r2.x)
или справа...
(r1.x > r2.x + r2.width)
или сверху...
(r1.y + r1.height < r2.y)
или внизу...
(r1.y > r2.y + r2.height)
второго прямоугольника, он не может столкнуться с ней. Поэтому, чтобы иметь функцию, которая возвращает логическое высказывание weather прямоугольники сталкиваются, мы просто объединяем условия по логическим ORs и отрицаем результат:
function checkOverlap(r1, r2) : Boolean
{
return !(r1.x + r1.width < r2.x || r1.y + r1.height < r2.y || r1.x > r2.x + r2.width || r1.y > r2.y + r2.height);
}
получить уже положительный результат при касании только мы можем изменить "" на "=".
задайте себе противоположный вопрос: Как я могу определить, не пересекаются ли два прямоугольника вообще? Очевидно, что прямоугольник A полностью слева от прямоугольника B не пересекается. Также, если A полностью справа. И аналогично, если A полностью выше B или полностью ниже B. В любом другом случае A и B пересекаются.
то, что ниже, может иметь ошибки, но я довольно уверен в алгоритме:
struct Rectangle { int x; int y; int width; int height; };
bool is_left_of(Rectangle const & a, Rectangle const & b) {
if (a.x + a.width <= b.x) return true;
return false;
}
bool is_right_of(Rectangle const & a, Rectangle const & b) {
return is_left_of(b, a);
}
bool not_intersect( Rectangle const & a, Rectangle const & b) {
if (is_left_of(a, b)) return true;
if (is_right_of(a, b)) return true;
// Do the same for top/bottom...
}
bool intersect(Rectangle const & a, Rectangle const & b) {
return !not_intersect(a, b);
}
предположим, что вы определили позиции и размеры прямоугольников вроде этого:
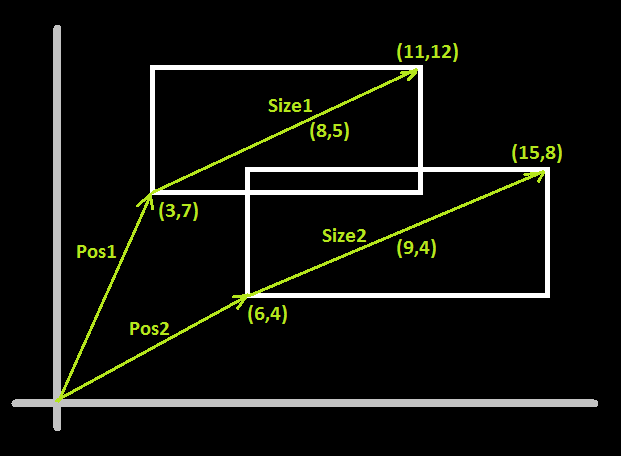
моя реализация C++ выглядит так:
class Vector2D
{
public:
Vector2D(int x, int y) : x(x), y(y) {}
~Vector2D(){}
int x, y;
};
bool DoRectanglesOverlap( const Vector2D & Pos1,
const Vector2D & Size1,
const Vector2D & Pos2,
const Vector2D & Size2)
{
if ((Pos1.x < Pos2.x + Size2.x) &&
(Pos1.y < Pos2.y + Size2.y) &&
(Pos2.x < Pos1.x + Size1.x) &&
(Pos2.y < Pos1.y + Size1.y))
{
return true;
}
return false;
}
пример вызова функции в соответствии с приведенным выше рисунком:
DoRectanglesOverlap(Vector2D(3, 7),
Vector2D(8, 5),
Vector2D(6, 4),
Vector2D(9, 4));
сравнения внутри if блок будет выглядеть следующим образом:
if ((Pos1.x < Pos2.x + Size2.x) &&
(Pos1.y < Pos2.y + Size2.y) &&
(Pos2.x < Pos1.x + Size1.x) &&
(Pos2.y < Pos1.y + Size1.y))
↓
if (( 3 < 6 + 9 ) &&
( 7 < 4 + 4 ) &&
( 6 < 3 + 8 ) &&
( 4 < 7 + 5 ))
вот как это делается в Java API:
public boolean intersects(Rectangle r) {
int tw = this.width;
int th = this.height;
int rw = r.width;
int rh = r.height;
if (rw <= 0 || rh <= 0 || tw <= 0 || th <= 0) {
return false;
}
int tx = this.x;
int ty = this.y;
int rx = r.x;
int ry = r.y;
rw += rx;
rh += ry;
tw += tx;
th += ty;
// overflow || intersect
return ((rw < rx || rw > tx) &&
(rh < ry || rh > ty) &&
(tw < tx || tw > rx) &&
(th < ty || th > ry));
}
struct Rect
{
Rect(int x1, int x2, int y1, int y2)
: x1(x1), x2(x2), y1(y1), y2(y2)
{
assert(x1 < x2);
assert(y1 < y2);
}
int x1, x2, y1, y2;
};
//some area of the r1 overlaps r2
bool overlap(const Rect &r1, const Rect &r2)
{
return r1.x1 < r2.x2 && r2.x1 < r1.x2 &&
r1.y1 < r2.y2 && r2.x1 < r1.y2;
}
//either the rectangles overlap or the edges touch
bool touch(const Rect &r1, const Rect &r2)
{
return r1.x1 <= r2.x2 && r2.x1 <= r1.x2 &&
r1.y1 <= r2.y2 && r2.x1 <= r1.y2;
}
в вопросе вы ссылаетесь на математику, когда прямоугольники находятся под произвольными углами поворота. Однако, если я понимаю бит об углах в вопросе, я интерпретирую, что все прямоугольники перпендикулярны друг другу.
общее знание области формулы перекрытия:
используя пример:
1 2 3 4 5 6
1 +---+---+
| |
2 + A +---+---+
| | B |
3 + + +---+---+
| | | | |
4 +---+---+---+---+ +
| |
5 + C +
| |
6 +---+---+
1) Соберите все координаты x (как слева, так и справа) в список, затем отсортируйте его и удалите дубликаты
1 3 4 5 6
2) соберите все координаты y (как сверху, так и снизу) в список, затем отсортируйте его и удалите дубликаты
1 2 3 4 6
3) Создайте 2D-массив по количеству промежутков между уникальными координатами x * количество промежутков между уникальными координатами Y.
4 * 4
4) Нарисуйте все прямоугольники в этой сетке, увеличивая количество каждой ячейки, над которой она происходит:
1 3 4 5 6
1 +---+
| 1 | 0 0 0
2 +---+---+---+
| 1 | 1 | 1 | 0
3 +---+---+---+---+
| 1 | 1 | 2 | 1 |
4 +---+---+---+---+
0 0 | 1 | 1 |
6 +---+---+
5) Как вы рисуете прямоугольники, его легко перехватить перекрытий.
предположим, что два прямоугольника-прямоугольник A и прямоугольник B. пусть центры будут A1 и B1 (координаты A1 и B1 можно легко найти), пусть высоты будут Ha и Hb, ширина-Wa и Wb, пусть dx-ширина(x) расстояние между A1 и B1 и dy-высота(y) расстояние между A1 и B1.
Теперь мы можем сказать, что A и B перекрываются: когда
если(!(dx > Wa+Wb)//!(dy > Ha+Hb)) возвращает true
самый простой способ-это
/**
* Check if two rectangles collide
* x_1, y_1, width_1, and height_1 define the boundaries of the first rectangle
* x_2, y_2, width_2, and height_2 define the boundaries of the second rectangle
*/
boolean rectangle_collision(float x_1, float y_1, float width_1, float height_1, float x_2, float y_2, float width_2, float height_2)
{
return !(x_1 > x_2+width_2 || x_1+width_1 < x_2 || y_1 > y_2+height_2 || y_1+height_1 < y_2);
}
прежде всего, подумайте, что в компьютерах система координат перевернута. ось x такая же, как в математике, но ось y увеличивается вниз и уменьшается при движении вверх.. если прямоугольник нарисован от центра. если координаты x1 больше, чем x2 плюс его половина widht. тогда это означает, что они будут касаться друг друга. и таким же образом идет вниз + половина его высоты. он столкнется..
я реализовал версию C#, она легко преобразуется в C++.
public bool Intersects ( Rectangle rect )
{
float ulx = Math.Max ( x, rect.x );
float uly = Math.Max ( y, rect.y );
float lrx = Math.Min ( x + width, rect.x + rect.width );
float lry = Math.Min ( y + height, rect.y + rect.height );
return ulx <= lrx && uly <= lry;
}
Не думайте о координатах как указывающих, где находятся пиксели. Считайте, что они находятся между пикселями. Таким образом, площадь прямоугольника 2x2 должна быть 4, а не 9.
bool bOverlap = !((A.Left >= B.Right || B.Left >= A.Right)
&& (A.Bottom >= B.Top || B.Bottom >= A.Top));
У меня есть очень простое решение
пусть x1,y1 x2 ,y2,l1,b1,l2-кординаты и их длины и ширины соответственно
рассмотрим условие ((x2
теперь этот прямоугольник будет перекрываться только в том случае,если диагональ точки x1,y1 будет лежать внутри другого прямоугольника или аналогично диагональ точки x2, y2 будет лежать внутри другого прямоугольника. именно это и подразумевает приведенное выше условие.
A и B два прямоугольника. С их охватывающий прямоугольник.
four points of A be (xAleft,yAtop),(xAleft,yAbottom),(xAright,yAtop),(xAright,yAbottom)
four points of A be (xBleft,yBtop),(xBleft,yBbottom),(xBright,yBtop),(xBright,yBbottom)
A.width = abs(xAleft-xAright);
A.height = abs(yAleft-yAright);
B.width = abs(xBleft-xBright);
B.height = abs(yBleft-yBright);
C.width = max(xAleft,xAright,xBleft,xBright)-min(xAleft,xAright,xBleft,xBright);
C.height = max(yAtop,yAbottom,yBtop,yBbottom)-min(yAtop,yAbottom,yBtop,yBbottom);
A and B does not overlap if
(C.width >= A.width + B.width )
OR
(C.height >= A.height + B.height)
Он заботится обо всех возможных случаях.
Это из упражнения 3.28 из книги Введение в Java Programming-Comprehensive Edition. Код проверяет, являются ли два прямоугольника indenticle, находится ли один внутри другого и находится ли один вне другого. Если ни одно из этих условий, то пересекаются.
* * 3.28 (геометрия: два прямоугольника) напишите программу, которая предложит пользователю ввести центр X-, Y-координаты, ширина и высота двух прямоугольников и определяет ли второй прямоугольник находится внутри первого или перекрывается с первым, как показано на рисунке на рис. Проверьте свою программу, чтобы охватить все случаи. Вот примеры выполнения:
введите координаты центра r1 x -, y -, ширину и высоту: 2.5 4 2.5 43 Введите координаты x-, y-центра r2, ширину и высоту: 1.5 5 0.5 3 r2 находится внутри r1
введите центр r1 x -, Y-координаты, ширина и высота: 1 2 3 5.5 Введите координаты x-, y-центра r2, ширину и высоту: 3 4 4.5 5 Р2 перекрывает Р1
введите координаты центра r1 x-, y -, ширину и высоту: 1 2 3 3 Введите координаты x-, y-центра r2, ширину и высоту: 40 45 3 2 r2 не перекрывает r1
import java.util.Scanner;
public class ProgrammingEx3_28 {
public static void main(String[] args) {
Scanner input = new Scanner(System.in);
System.out
.print("Enter r1's center x-, y-coordinates, width, and height:");
double x1 = input.nextDouble();
double y1 = input.nextDouble();
double w1 = input.nextDouble();
double h1 = input.nextDouble();
w1 = w1 / 2;
h1 = h1 / 2;
System.out
.print("Enter r2's center x-, y-coordinates, width, and height:");
double x2 = input.nextDouble();
double y2 = input.nextDouble();
double w2 = input.nextDouble();
double h2 = input.nextDouble();
w2 = w2 / 2;
h2 = h2 / 2;
// Calculating range of r1 and r2
double x1max = x1 + w1;
double y1max = y1 + h1;
double x1min = x1 - w1;
double y1min = y1 - h1;
double x2max = x2 + w2;
double y2max = y2 + h2;
double x2min = x2 - w2;
double y2min = y2 - h2;
if (x1max == x2max && x1min == x2min && y1max == y2max
&& y1min == y2min) {
// Check if the two are identicle
System.out.print("r1 and r2 are indentical");
} else if (x1max <= x2max && x1min >= x2min && y1max <= y2max
&& y1min >= y2min) {
// Check if r1 is in r2
System.out.print("r1 is inside r2");
} else if (x2max <= x1max && x2min >= x1min && y2max <= y1max
&& y2min >= y1min) {
// Check if r2 is in r1
System.out.print("r2 is inside r1");
} else if (x1max < x2min || x1min > x2max || y1max < y2min
|| y2min > y1max) {
// Check if the two overlap
System.out.print("r2 does not overlaps r1");
} else {
System.out.print("r2 overlaps r1");
}
}
}
bool Square::IsOverlappig(Square &other)
{
bool result1 = other.x >= x && other.y >= y && other.x <= (x + width) && other.y <= (y + height); // other's top left falls within this area
bool result2 = other.x >= x && other.y <= y && other.x <= (x + width) && (other.y + other.height) <= (y + height); // other's bottom left falls within this area
bool result3 = other.x <= x && other.y >= y && (other.x + other.width) <= (x + width) && other.y <= (y + height); // other's top right falls within this area
bool result4 = other.x <= x && other.y <= y && (other.x + other.width) >= x && (other.y + other.height) >= y; // other's bottom right falls within this area
return result1 | result2 | result3 | result4;
}
для тех из вас, кто использует центральные точки и половинные размеры для своих данных прямоугольника, вместо типичных x,y,w, h или x0,y0,x1,x1, вот как вы можете это сделать:
#include <cmath> // for fabsf(float)
struct Rectangle
{
float centerX, centerY, halfWidth, halfHeight;
};
bool isRectangleOverlapping(const Rectangle &a, const Rectangle &b)
{
return (fabsf(a.centerX - b.centerX) <= (a.halfWidth + b.halfWidth)) &&
(fabsf(a.centerY - b.centerY) <= (a.halfHeight + b.halfHeight));
}
"Если вы выполняете вычитание координат x или y, соответствующих вершинам двух, обращенных к каждому прямоугольнику, если результаты одинаковы, два прямоугольника не перекрывают оси, которые" (извините, я не уверен, что мой перевод правильный)

источник:http://www.ieev.org/2009/05/kiem-tra-hai-hinh-chu-nhat-chong-nhau.html
Java-код, чтобы выяснить, контактируют ли прямоугольники или перекрывают друг друга
...
for (int i = 0;i < n;i++) {
for (int j = 0;j < n; j++) {
if (i != j) {
Rectangle rectangle1 = rectangles.get(i);
Rectangle rectangle2 = rectangles.get(j);
int l1 = rectangle1.l; //left
int r1 = rectangle1.r; //right
int b1 = rectangle1.b; //bottom
int t1 = rectangle1.t; //top
int l2 = rectangle2.l;
int r2 = rectangle2.r;
int b2 = rectangle2.b;
int t2 = rectangle2.t;
boolean topOnBottom = t2 == b1;
boolean bottomOnTop = b2 == t1;
boolean topOrBottomContact = topOnBottom || bottomOnTop;
boolean rightOnLeft = r2 == l1;
boolean leftOnRight = l2 == r1;
boolean rightOrLeftContact = leftOnRight || rightOnLeft;
boolean leftPoll = l2 <= l1 && r2 >= l1;
boolean rightPoll = l2 <= r1 && r2 >= r1;
boolean leftRightInside = l2 >= l1 && r2 <= r1;
boolean leftRightPossiblePlaces = leftPoll || rightPoll || leftRightInside;
boolean bottomPoll = t2 >= b1 && b2 <= b1;
boolean topPoll = b2 <= b1 && t2 >= b1;
boolean topBottomInside = b2 >= b1 && t2 <= t1;
boolean topBottomPossiblePlaces = bottomPoll || topPoll || topBottomInside;
boolean topInBetween = t2 > b1 && t2 < t1;
boolean bottomInBetween = b2 > b1 && b2 < t1;
boolean topBottomInBetween = topInBetween || bottomInBetween;
boolean leftInBetween = l2 > l1 && l2 < r1;
boolean rightInBetween = r2 > l1 && r2 < r1;
boolean leftRightInBetween = leftInBetween || rightInBetween;
if ( (topOrBottomContact && leftRightPossiblePlaces) || (rightOrLeftContact && topBottomPossiblePlaces) ) {
path[i][j] = true;
}
}
}
}
...
этот ответ должен быть лучший ответ:
Если прямоугольники перекрываются, то площадь перекрытия будет больше нуля. Теперь давайте найдем область перекрытия:
если они перекрываются, то левый край перекрытия-rect будет max (r1.Х1,Р2.x1) и правый край будет min (r1.x2, r2.x2). таким образом, длина перекрытия будет min(r1.x2, r2.x2) - max (r1.Х1,Р2.x1)
таким образом, площадь будет: area = (max (r1.Х1, Р2.x1) - min (r1.x2, r2.x2)) * (max(r1.У1, Р2.У1) - min(r1.У2, Р2.y2))
Если area = 0, то они не перекрываются. Просто, не так ли?
